题目内容
1．一个不透明的口袋中装有4个分别标有数字-1，-2，3，4的小球，它们的形状、大小完全相同．小红先从口袋中随机摸出一个小球记下数字为x；小颖在剩下的3个小球中随机摸出一个小球记下数字为y．（1）小红摸出标有数字3的小球的概率是$\frac{1}{4}$；
（2）请用列表法或画树状图的方法表示出由x，y确定的点P（x，y）所有可能的结果，并求出点P（x，y）落在第三象限的概率．
分析 （1）直接根据概率公式求解即可；
（2）首先通过列表展示所有12种等可能性的结果数，再找出在第一象限或第三象限的结果数和第二象限或第四象限的结果数，然后根据概率公式计算两人获胜的概率即可．
解答 解：
（1）小红摸出标有数字3的小球的概率是$\frac{1}{4}$；
故答案为：$\frac{1}{4}$；
（2）列表如下：
| -1 | -2 | 3 | 4 | |
| -1 | （-1，-2） | （-1，3） | （-1，4） | |
| -2 | （-2，-1） | （-2，3） | （-2，4） | |
| 3 | （3，-1） | （3，-2） | （3，4） | |
| 4 | （4，-1） | （4，-2） | （4，3） |
所以P（点P落在第三象限）=$\frac{2}{12}$=$\frac{1}{6}$．
点评 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
11．下列各度数不是多边形的内角和的是（ ）
| A． | 1700° | B． | 540° | C． | 1800° | D． | 10800° |
如图是由5个高和底面直径相等的圆柱体搭成的立体图形，这个立体图形的左视图是（ ）
9．
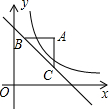如图，过点A（4，5）分别作x轴、y轴的平行线，交直线y=-x+6于B、C两点，若函数y=$\frac{k}{x}$（x＞0）的图象△ABC的边有公共点，则k的取值范围是（ ）
如图，过点A（4，5）分别作x轴、y轴的平行线，交直线y=-x+6于B、C两点，若函数y=$\frac{k}{x}$（x＞0）的图象△ABC的边有公共点，则k的取值范围是（ ）| A． | 5≤k≤20 | B． | 8≤k≤20 | C． | 5≤k≤8 | D． | 9≤k≤20 |
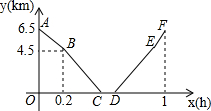从甲地到乙地，先是一段上坡路，然后是一段平路，小明骑车从甲地出发，到达乙地后休息一段时间，然后原路返回甲地．假设小明骑车在上坡、平路、下坡时分别保持匀速前进，已知小明骑车上坡的速度比平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km，设小明出发xh后，到达离乙地ykm的地方，图中的折线ABCDEF表示y与x之间的函数关系．
6．为了解某班学生每天使用零花钱的情况，小明随机查了15名同学，结果如下表：
关于这15名同学每天使用的零花钱，下列说法正确的是（ ）
| 每天使用零花钱（单位：元） | 0 | 1 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 5 | 4 | 2 |
| A． | 众数是5元 | B． | 极差是4元 | C． | 中位数3元 | D． | 平均数是2.5元 |
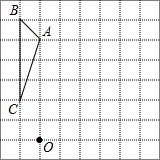如图，方格纸中的每个小方格都是边长为1的正方形，△ABC的顶点都在格点上，请完成下列任务：
