题目内容
求证:等腰三角形底边上的中点到两腰的距离相等.
请按以下解题步骤完成证明过程:
步骤一:按题意画出图形;
步骤二:结合图形,写出已知、求证;
步骤三:写出证明过程.
请按以下解题步骤完成证明过程:
步骤一:按题意画出图形;
步骤二:结合图形,写出已知、求证;
步骤三:写出证明过程.
考点:等腰三角形的性质
专题:证明题
分析:证明命题时,首先根据题意画出图形,再结合图形写出已知及求证的内容,然后利用已学知识进行证明.
解答:已知:在△ABC中,AB=AC,点D是BC边的中点,DE⊥AB于点E,DF⊥AC于点F.
求证:DE=DF.

证明:∵AB=AC,
∴∠B=∠C.
∵点D是BC边的中点,
∴DB=DC.
又∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
在Rt△DEB与Rt△DFC中,
∴Rt△DEB≌Rt△DFC(AAS),
∴DE=DF.
求证:DE=DF.

证明:∵AB=AC,
∴∠B=∠C.
∵点D是BC边的中点,
∴DB=DC.
又∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
在Rt△DEB与Rt△DFC中,
|
∴Rt△DEB≌Rt△DFC(AAS),
∴DE=DF.
点评:本题主要考查命题的证明步骤,等腰三角形的性质及全等三角形的性质与判定.根据命题画出图形是解题的关键.

练习册系列答案
相关题目
 如图,将边长为4cm的正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动三次后,正方形ABCD的中心O所经过的路线长是
如图,将边长为4cm的正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动三次后,正方形ABCD的中心O所经过的路线长是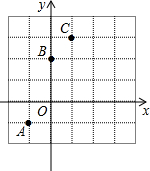 如图,已知二次函数y=ax2+bx+2的图象经过A(-1,-1),C(1,3).
如图,已知二次函数y=ax2+bx+2的图象经过A(-1,-1),C(1,3).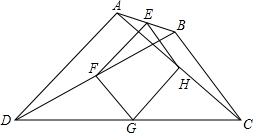 在四边形ABCD中,E、F、G、H分别是AB、BD、DC、AC的中点.
在四边形ABCD中,E、F、G、H分别是AB、BD、DC、AC的中点. 如图,在所给正方形网格中完成下列各题:(用直尺画图,保留痕迹)
如图,在所给正方形网格中完成下列各题:(用直尺画图,保留痕迹) 如图,在⊙O中,半径OC⊥弦AB,垂足为D,AB=8,CD=2,求○O的半径.
如图,在⊙O中,半径OC⊥弦AB,垂足为D,AB=8,CD=2,求○O的半径.