题目内容
13.计算:(1)1+(-5)
(2)$-{1^2}÷4+3×(-\frac{1}{6})$
(3)$({-\frac{7}{12}+\frac{5}{9}-\frac{1}{6}})×36$
(4)$\sqrt{49}+\root{3}{-27}-\sqrt{{{(-2)}^2}}$.
分析 (1)原式利用异号两数相加的法则计算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)原式利用乘法分配律计算即可得到结果;
(4)原式利用算术平方根及立方根定义计算即可得到结果.
解答 解:(1)原式=1-5=-4;
(2)原式=-$\frac{1}{4}$-$\frac{1}{2}$=-$\frac{3}{4}$;
(3)原式=-21+20-6-27+20=-7;
(4)原式=7+(-3)-2=7-3-2=7-5=2.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3. 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )| A. | 甲乙两人8分钟各跑了800米 | |
| B. | 前2分钟,乙的平均速度比甲快 | |
| C. | 5分钟时两人都跑了500米 | |
| D. | 甲跑完800米的平均速度为100米∕分 |
8.下列说法正确的是( )
| A. | 带有“+”号的数是正数 | |
| B. | 带有“-”号的数是负数 | |
| C. | 数轴上的两个点可以表示同一个有理数 | |
| D. | 有理数分为自然数、负整数、分数 |
18.已知(x-3)2+$\sqrt{y+1}$=0,则x+y的值为( )
| A. | 2 | B. | -1 | C. | 1 | D. | 5 |
2.在锐角的内部引射线,当n=1,n=2时,图中小于180°角的个数及规律如表,请你在表中空白处填出射线为3和n的情形.
| 图形 |  | 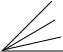 | 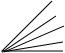 | 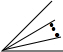 |
| n | 1 | 2 | 3 | n |
| 个数及规律 | 3=1+2=$\frac{2×3}{2}$ | 6=1+2+3=$\frac{3×4}{2}$ | 10=1+2+3+4=$\frac{4×5}{2}$ | 1+2+3+…+n+1=$\frac{(n+1)(n+2)}{2}$. |
 如图,一块矩形的土地,长48m,宽24m,要在它的中央划一块矩形的草地,四周铺上花砖路,路面宽都相等,草地占去矩形土地的$\frac{5}{9}$,则花砖路面的宽为多少?
如图,一块矩形的土地,长48m,宽24m,要在它的中央划一块矩形的草地,四周铺上花砖路,路面宽都相等,草地占去矩形土地的$\frac{5}{9}$,则花砖路面的宽为多少?