题目内容
6. 如图,直线DE与直线DF交于点D,△ABC与△A′B′C′关于DE对称.
如图,直线DE与直线DF交于点D,△ABC与△A′B′C′关于DE对称.(1)作△A′B′C关于直线DF对称的△A″B″C″;
(2)试探索∠BDB″与∠EDF之间的关系,并加以证明.
分析 (1)分别作出点A′、B′、C′关于直线DF的对称点A″、B″、C″即可得到△A″B″C″;
(2)理由对称的性质得∠BDE=∠B′DE,∠B′DG=∠B″DG,利用周角定理得到∠BDB″=360°-(∠BDE-∠B′DE-∠B′DG-∠B″DG),然后利用等量代换可得∠BDB″=360°-2∠EDG,再利用邻补角定义可得到∠BDB″与∠EDF之间的关系.
解答 解:(1)如图,△A″B″C″为所求;
(2)∠BDB″=2∠EDF.理由如下:
∵△ABC与△A′B′C′关于DE对称.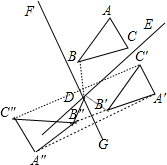
∴∠BDE=∠B′DE,
∵△A′B′C与△A″B″C″关于DF对称,
∴∠B′DG=∠B″DG,
∴∠BDB″=360°-(∠BDE-∠B′DE-∠B′DG-∠B″DG)
=360°-(2∠B′DE-2∠B′DG)
=360°-2∠EDG
=360°-2(180°-∠EDF)
=2∠EDF.
点评 本题考查了作图-轴对称变换:几何图形都可看做是有点组成,我们在画一个图形的轴对称图形时,可以确定一些特殊的对称点.也考查了对称轴的性质.

练习册系列答案
相关题目
16.据有关资料显示,2014年末,盐城全市户籍人口828.5万人,将828.5万用科学记数法可表示为( )
| A. | 8.285×103 | B. | 828.5×104 | C. | 8.285×105 | D. | 8.285×106 |
11.若y=$\frac{1}{\sqrt{4-x}}$有意义,则x的取值范围是( )
| A. | x≠4 | B. | x≤4 | C. | x≥4 | D. | x<4 |