题目内容
3．下面的图表是我国数学家发明的“杨辉三角”，此图揭示了（a+b）n（n为非负整数）的展开式的项数及各项系数的有关规律．请你观察，并根据此规律写出：（a-b）7的第5项的系数是35．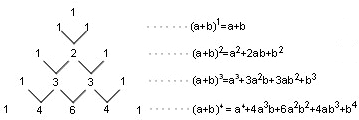
分析 根据“杨辉三角”，寻找解题的规律．
解答 解：根据规律，（a+b）7的展开式共有8项，
各项系数依次为1，-7，21，-35，35，-21，7，-1，
故第5项的系数是35，
故答案为35．
点评 本题考查了完全平方公式．关键是由“杨辉三角”图，由易到难，发现一般规律．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
16．定义：a是不为1的有理数，我们把$\frac{1}{1-a}$称为a的差倒数，如2的差倒数是$\frac{1}{1-2}$=-1，-1的差倒数是$\frac{1}{1-（-1）}$=$\frac{1}{2}$．已知a1=-$\frac{1}{2}$，a2是a1的差倒数，a3是a2的差倒数，a4是 a3的差倒数，…，以此类推，则a2016为（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | 3 | D． | 1 |
如图，在平面直角坐标系中，点A的坐标为（0，2），点p的坐标为（m，0）且m＞0，一开口向上的抛物线以P为顶点，且经过点A．
18．在密码学中，把直接可以看到的内容称为明码，对明码进行某种处理后得到的内容称为密码．有一种密码，将英文26个字母a，b，c，…z依次对应1、2、3，…，26这26个自然数，如下表，当明码对应的序号x为奇数时，密码对应的序号y=$\frac{x+1}{2}$；当明码对应的序号x为偶数时，密码对应的序号y=$\frac{x}{2}+13$．
按上述规定，将明码“love”译成密码（密码是字母）是s、h、x、c．
| 字母 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 序号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
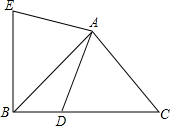在等腰Rt△ABC中，∠A=90°，AC=AB=2，D是BC边上的点且BD=$\frac{1}{3}$CD，连接AD，把AD绕着点A顺时针旋转90°得到线段AE，连接BE，则点B到AD的距离为$\frac{\sqrt{10}}{5}$．
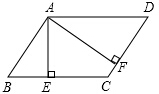如图，在平行四边形ABCD中，AE⊥BC，AF⊥CD，若平行四边形ABCD的周长为48，AE=5，AF=10，则平行四边形ABCD的面积是80．
12．下列关于平角和周角的说法正确的是（ ）
| A． | 平角是一条线段 | B． | 周角是一条射线 | ||
| C． | 两个锐角的和不一定小于平角 | D． | 反向延长射线OA，就形成一个平角 |
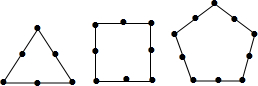墨墨用黑色的棋子摆各种正多边形，如图所示，他摆正三角形的时候用了6个棋子，摆正方形的时候用了8个棋子，摆正五边形的时候用了10个棋子，以此类推，当墨墨摆完正十二边形时，共用了150个棋子．