题目内容
8.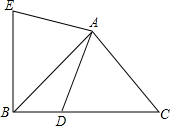 在等腰Rt△ABC中,∠A=90°,AC=AB=2,D是BC边上的点且BD=$\frac{1}{3}$CD,连接AD,把AD绕着点A顺时针旋转90°得到线段AE,连接BE,则点B到AD的距离为$\frac{\sqrt{10}}{5}$.
在等腰Rt△ABC中,∠A=90°,AC=AB=2,D是BC边上的点且BD=$\frac{1}{3}$CD,连接AD,把AD绕着点A顺时针旋转90°得到线段AE,连接BE,则点B到AD的距离为$\frac{\sqrt{10}}{5}$.
分析 作AN⊥BC于N,BM⊥AD于M,根据$\frac{1}{2}$•BD•AN=$\frac{1}{2}$•AD•BM即可解决问题.
解答 解:如图,作 AN⊥BC于N,BM⊥AD于M.
AN⊥BC于N,BM⊥AD于M.
∵AB=AC=2,∠BAC=90°,
∴BC=2$\sqrt{2}$,AN=BN=NC=$\sqrt{2}$,
∵BD=$\frac{1}{3}$CD,
∴BD=DN=$\frac{\sqrt{2}}{2}$,AD=$\sqrt{A{N}^{2}+D{N}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{10}}{2}$,
∵$\frac{1}{2}$•BD•AN=$\frac{1}{2}$•AD•BM,
∴$\frac{\sqrt{2}}{2}$•$\sqrt{2}$=$\frac{\sqrt{10}}{2}$•BM,
∴BM=$\frac{\sqrt{10}}{5}$.
故答案为$\frac{\sqrt{10}}{5}$.
点评 本题考查等腰直角三角形的性质、勾股定理等知识,解题的关键是利用面积法求高,属于中考常考题型.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
1.实数-6的倒数是( )
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | -6 | D. | 6 |
 已知:如图,在平面直角坐标系中,一次函数y=$\frac{1}{2}$x-1的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A(4,n)、B(m,-2)两点.
已知:如图,在平面直角坐标系中,一次函数y=$\frac{1}{2}$x-1的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A(4,n)、B(m,-2)两点.
 如图,在直角坐标系xOy中,直线l:y=ax+b交x轴于点A(-2,0),交y轴于点B(0,2),半径为$\sqrt{2}$的⊙P与x轴相切于点C($\sqrt{2}$,0).
如图,在直角坐标系xOy中,直线l:y=ax+b交x轴于点A(-2,0),交y轴于点B(0,2),半径为$\sqrt{2}$的⊙P与x轴相切于点C($\sqrt{2}$,0).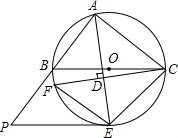 如图,△ABC是⊙O的内接三角形,BC是⊙O的直径,AE是⊙O的弦,点F是弧BE上一点,且AE⊥CF,垂足是D,⊙O的切线PE交AB的延长线于点P,
如图,△ABC是⊙O的内接三角形,BC是⊙O的直径,AE是⊙O的弦,点F是弧BE上一点,且AE⊥CF,垂足是D,⊙O的切线PE交AB的延长线于点P,