题目内容
4.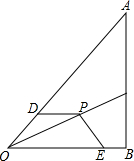 如图,点P为OC上一点,PD=PE,∠0DP+∠OEP=180°,求证:0P平分∠A0B.
如图,点P为OC上一点,PD=PE,∠0DP+∠OEP=180°,求证:0P平分∠A0B.
分析 作PF⊥OA于点F,PG⊥OB于G,证出∠OEP=∠FDP,由AAS证明△PDF≌△PGE,得出PF=PG,即可得出结论.
解答 证明:作PF⊥OA于点F,PG⊥OB于G,如图所示: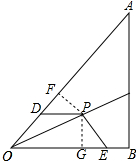
∵∠ODP+∠OEP=180°,∠ODP+∠FDP=180°,
∴∠OEP=∠FDP,
在△PDF和△PGE中,
$\left\{\begin{array}{l}{∠OEP=∠FDP}\\{∠PFD=∠PGE=90°}\\{PD=PE}\end{array}\right.$,
∴△PDF≌△PGE(AAS),
∴PF=PG,
∴OP平分∠AOB.
点评 本题考查了全等三角形的判定与性质、角平分线的判定;熟练掌握角平分线的判定方法,证明三角形全等得出PF=PG是解决问题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
16.对于函数y=-$\frac{5}{x}$,下列说法错误的是( )
| A. | 它的图象分布在二、四象限 | |
| B. | 它的图象既是轴对称图形又是中心对称图形 | |
| C. | 当x>0时,y的值随x的增大而增大 | |
| D. | 当x<0时,y的值随x的增大而减小 |
1.下列说法正确的是( )
| A. | 若a>0,b>0,则$\frac{a}{b}$>0 | B. | 若$\frac{a}{b}$>0,则a<0,b<0, | ||
| C. | 若a•b=0,则a=0且b=0 | D. | 若a•b>0,则a>0,b>0 |
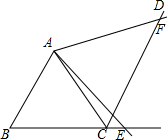 已知,如图,△ABC为等边三角形,CD∥AB,点E、F分别在BC延长线及CD上,∠EAF=60°,求证:BE=CF.
已知,如图,△ABC为等边三角形,CD∥AB,点E、F分别在BC延长线及CD上,∠EAF=60°,求证:BE=CF.
 如图所示.点C、D在线段AB上,且点D是线段CB的中点.
如图所示.点C、D在线段AB上,且点D是线段CB的中点.