题目内容
14.已知直线y=kx+b经过点P(5,1),Q(-1,-5).(1)求k和b的值;
(2)已知点A(m,-3)在该直线上,求直线上所有位于点A朝上一侧的点的横坐标的取值范围与纵坐标的取值范围;
(3)对于直线上一点B(x,y),当x取何值时,y>4?
分析 (1)已知直线y=kx+b经过点P(5,1)和点Q(-1,-5),代入可求出k,b的值;
(2)求得A点的坐标,然后根据一次函数的性质即可求得
(3)求得y=4时的函数值,根据一次函数的性质即可求得.
解答 解:(1)∵直线y=kx+b经过点P(5,1),Q(-1,-5),
∴$\left\{\begin{array}{l}{5k+b=1}\\{-k+b=-5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-4}\end{array}\right.$.
故k=1,b=-4.
(2)∵点A(m,-3)在该直线上,
∴-3=m-4,解得m=1,
∴A(1,-3),
∵k=1>0,
∴y随x的增大而增大,
∴直线上所有位于点A朝上一侧的点的横坐标的取值范围是x>1,纵坐标的取值范围是x>-3.
(3)∵一次函数为y=x-4,
∴当y=4时,则x=8,
∴当x>8时,y>4.
点评 本题考查了待定系数法求一次函数的解析式以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解题的关键.

练习册系列答案
相关题目
5.对于两个实数a,b,用max(a,b)表示其中较大的数,则方程x×max(x,-x)=2x+1的解是( )
| A. | 1,1+$\sqrt{2}$ | B. | 1,1-$\sqrt{2}$ | C. | -1,1+$\sqrt{2}$ | D. | -1,1-$\sqrt{2}$ |
2.等腰三角形的周长为12cm,其中一边长为5cm,则该等腰三角形的底边为( )
| A. | 5cm | B. | 3cm | C. | 3.5cm或2cm | D. | 8cm |
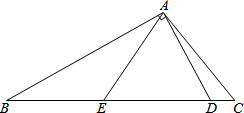 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.
如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.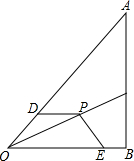 如图,点P为OC上一点,PD=PE,∠0DP+∠OEP=180°,求证:0P平分∠A0B.
如图,点P为OC上一点,PD=PE,∠0DP+∠OEP=180°,求证:0P平分∠A0B.