题目内容
已知二次函数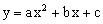 图象的顶
图象的顶 点横坐标是4,与x轴交于A(x1,0)、B(x2,0),x1﹤0﹤x2,与y轴交于点C,O为坐标原点,
点横坐标是4,与x轴交于A(x1,0)、B(x2,0),x1﹤0﹤x2,与y轴交于点C,O为坐标原点,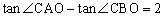 。
。
(1)求证:  ;
;
(2)求a、b的值;
(3)若二次函数图象与直线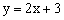
 仅有一个交点时,求二次函数的最值。
仅有一个交点时,求二次函数的最值。
(1)∵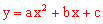 图象的顶点横坐标是4,
图象的顶点横坐标是4,
∴抛物线的对称轴为x=4, 即
即 ,化简得:
,化简得: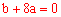 。
。
(2)∵二次函数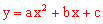 与x轴交于A(x1,0)、B(x2,0),x1<0<x2,
与x轴交于A(x1,0)、B(x2,0),x1<0<x2,
∴OA=-x1,OB=x2;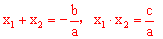 。
。
令x=0,得y =c,∴C(0,c),∴OC=|c|。
=c,∴C(0,c),∴OC=|c|。
由三角函数定义得:
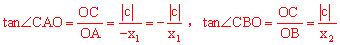 。
。
∵tan∠CAO-tan∠CBO=2,即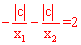 ,化简得:
,化简得: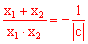 。
。
将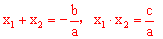 代入得:
代入得: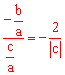 ,化简
,化简 得:
得: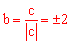 。
。
由(1)知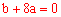 ,
,
∴当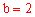 时,
时,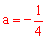 ;当
;当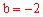 时,
时,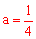 。
。
∴a、b的值为: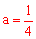 ,
, 或
或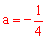 ,
,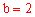 。
。
(3)①由(2)知,当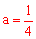 ,
, 时,抛物线解析式为:
时,抛物线解析式为: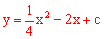 。
。
联立抛物线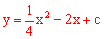 与直线
与直线 解析式得到:
解析式得到: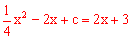 ,
,
化简得: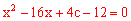 。
。
∵二次函数图象与直线 仅有一个交点,
仅有一个交点,
∴一元二次方程根的判别式 等于0,即
等于0,即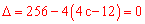 ,解得
,解得 =19。
=19。
∴抛物线解析式为: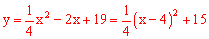 。
。
当x=4时,二次函数有最小值,最小值为15。
②由(2)知,当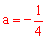 ,
,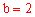 时,抛物线解析式为:
时,抛物线解析式为: 。
。
联立抛物线 与直线
与直线 解析式得到:
解析式得到: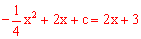 ,
,
化简得 :
: 。
。
∵二次函数图象与直线 仅有一个交点,
仅有一个交点,
∴一元二次方程根的判别式等于0,即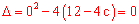 ,解得
,解得 =3。
=3。
∴抛物线解析式为: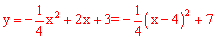 。
。
当x=4时,二次函数有最大值,最大值为7。
综上所述,若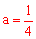 ,
, ,
, =19,二次函数图象与直线
=19,二次函数图象与直线 仅有一个交点时,二次函数的最小值为15;若
仅有一个交点时,二次函数的最小值为15;若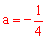 ,
,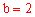 ,
, =3,二次函数图象与
=3,二次函数图象与 直线
直线 仅有一个交点时,二次函数的最大值为7。
仅有一个交点时,二次函数的最大值为7。
【考点】二次函数综合题,曲线上点的坐标与方程的关系,一元二次方程根的判别式和根与系数的关系,锐角三角函数定义,二次函数的性质,分类思想的应用。


练习册系列答案
相关题目
 的值为 ( )
的值为 ( )
 的图象与正比例函数
的图象与正比例函数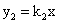
 的图象交于点(2,1),则使y1>y2的x的取值范围是【 】
的图象交于点(2,1),则使y1>y2的x的取值范围是【 】

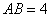
 ,点
,点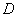
 的坐标是
的坐标是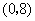
 ,以点
,以点
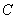
 为顶点的抛物线
为顶点的抛物线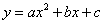
 经过
经过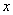
 轴上的点
轴上的点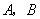
 .
.

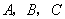
 的坐标;
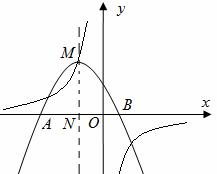
的坐标;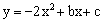 图像的顶点M在反比例函数
图像的顶点M在反比例函数 上,且与
上,且与 轴交于A,B两点。
轴交于A,B两点。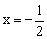 ,试
,试 求
求 的值,并求AB的长;
的值,并求AB的长;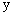 轴左侧,与
轴左侧,与
 正六边形靶子上随意抛一枚飞镖,则飞镖插不落在阴影区域的概率为【 】
正六边形靶子上随意抛一枚飞镖,则飞镖插不落在阴影区域的概率为【 】
 B.
B.  C.
C.  D.
D. 
 ,AC=
,AC= ,BC=6,点M在AB边上,且AM=
,BC=6,点M在AB边上,且AM= BM,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长。
BM,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长。
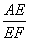
 =3,求
=3,求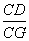
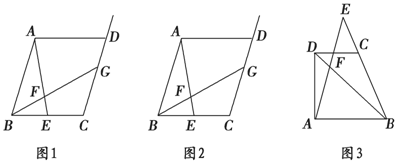

 :
: 的值是________(用含有m的代数式表示),试写出解答过程.
的值是________(用含有m的代数式表示),试写出解答过程.

 AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .