题目内容
如图,已知二次函数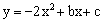 图像的顶点M在反比例函数
图像的顶点M在反比例函数 上,且与
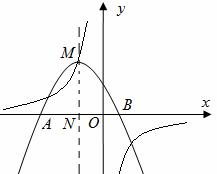
上,且与 轴交于A,B两点。
轴交于A,B两点。
(1)若二次函数的对称轴为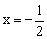 ,试
,试 求
求 的值,并求AB的长;
的值,并求AB的长;
(2)若二次函数的对称轴在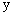 轴左侧,与
轴左侧,与
 轴的交点为N,当NO+MN取最小值时,试求二次函数的解析式。
轴的交点为N,当NO+MN取最小值时,试求二次函数的解析式。
(1)∵二次函数的对称轴为 ,
,
∴ 。
。
∴二次函数的顶点为M( )。
)。
∵顶点M在反比例函数 上,∴
上,∴ ,解得
,解得 。
。
∴二次函数的解析式为 。
。
(2)∵二次函数的解析式为 ,
,
∴令 =0,得
=0,得
 ,解得
,解得 。
。
∴AB= 。
。
(3)∵二次函数的对称轴为 ,且当
,且当 时,
时, M点坐标为(
M点坐标为( )。
)。
∴NO+MN ,
,
即2是NO+MN的最小值。
此时,
 ,解得
,解得 。
。
∴M点坐标为( )。
)。
∴此时二次函数的解析式为 ,即
,即 。
。
【考点】二次函数综合题,二次函数的对称轴和顶点性质,曲线上点的坐标与方程的关系,解一元二次方程,不等式的性质。

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 中点上,将直角三角板DEF绕D点按逆时针方向旋转。
中点上,将直角三角板DEF绕D点按逆时针方向旋转。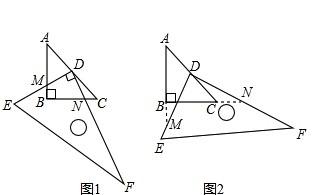

 ,某学校对教室采用药熏清毒法进行消毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比
,某学校对教室采用药熏清毒法进行消毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比 例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,
例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息, 解答下列问题:
解答下列问题:

 进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室;
进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室; 中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么? 当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面AC共需
当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面AC共需  秒.
秒.

 数
数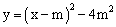
 (m>0)的图象与x轴交于A、B两点.
(m>0)的图象与x轴交于A、B两点.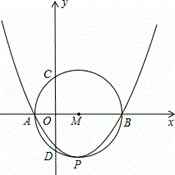

 B为直径的圆上,求二次函数的解析式;
B为直径的圆上,求二次函数的解析式;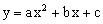 图象的顶
图象的顶 点横坐标是4,与x轴交于A(x1,0)、B(x2,0),x1﹤0﹤x2,与y轴交于点C,O为坐标原点,
点横坐标是4,与x轴交于A(x1,0)、B(x2,0),x1﹤0﹤x2,与y轴交于点C,O为坐标原点,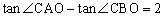 。
。 ;
;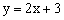
 仅有一个交点时,求二次函数的最值。
仅有一个交点时,求二次函数的最值。

 任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形的面积为2的概率;
任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形的面积为2的概率; 的一点M,求以A、B、M为顶点的三角形为直角三角形的概率.
的一点M,求以A、B、M为顶点的三角形为直角三角形的概率.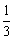 AD,延长M
AD,延长M D至点E,使ME=MB,以DE为边作正方形DEFG,点G在边CD上,则
D至点E,使ME=MB,以DE为边作正方形DEFG,点G在边CD上,则 DG 的长为 。
DG 的长为 。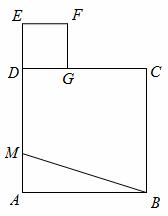

 B.
B. C.
C. 8 D.
8 D.