题目内容
 如图,线段AB=10cm,点C为线段A上一点,BC=3cm,点D,E分别为AC和AB的中点,求线段DE的长.
如图,线段AB=10cm,点C为线段A上一点,BC=3cm,点D,E分别为AC和AB的中点,求线段DE的长.考点:两点间的距离
专题:
分析:根据线段的和差,可得AC的长,根据线段中点的性质,可得AD、AE的长,根据线段的和差,可得DE的长.
解答:解:由线段的和差,得
AC=AB-BC=10-3=7cm,
由点D是AC的中点,
所以AD=
AC=
×7=
cm;
由点E是AB的中点,得
AE=
AB=
×10=5cm,
由线段的和差,得
DE=AE-AD=5-
=
cm.
AC=AB-BC=10-3=7cm,
由点D是AC的中点,
所以AD=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
由点E是AB的中点,得
AE=
| 1 |
| 2 |
| 1 |
| 2 |
由线段的和差,得
DE=AE-AD=5-
| 7 |
| 2 |
| 3 |
| 2 |
点评:本题考查了两点间的距离,利用了线段的和差,线段中点的性质.

练习册系列答案
相关题目
直线l与半径为r的⊙O相交,且点O到直线l的距离为5,则r的取值范围是( )
| A、r<5 | B、r=5 |
| C、r>5 | D、r≥5 |
 (1)已知线段a,b.用圆规和直尺作线段AC,及线段AC上的点B,使AC=2a+b,其中AB=2a,BC=b.(不写作法但保留作图痕迹);
(1)已知线段a,b.用圆规和直尺作线段AC,及线段AC上的点B,使AC=2a+b,其中AB=2a,BC=b.(不写作法但保留作图痕迹);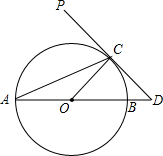 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD. 如图,B、C两点把线段AD分成2,4,3三部分,点P是AD的中点,已知CD=5,求线段PC的长.
如图,B、C两点把线段AD分成2,4,3三部分,点P是AD的中点,已知CD=5,求线段PC的长.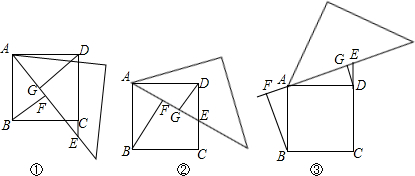
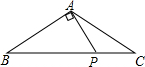 已知,如图,△ABC中,AB=AC,∠BAC=120°,P是BC上的点且PA⊥AB,求证:AP=PC.
已知,如图,△ABC中,AB=AC,∠BAC=120°,P是BC上的点且PA⊥AB,求证:AP=PC.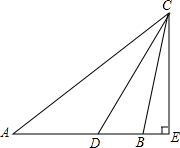 如图,△ABC中,AB=BC,CD平分∠ACB,CE⊥AB于E,若∠DCE=30°,求△ABC各角的度数.
如图,△ABC中,AB=BC,CD平分∠ACB,CE⊥AB于E,若∠DCE=30°,求△ABC各角的度数.