题目内容
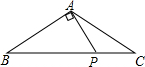已知，如图，△ABC中，AB=AC，∠BAC=120°，P是BC上的点且PA⊥AB，求证：AP=PC．考点：等腰三角形的判定与性质
专题：
分析：先求出∠C=30°，再求出∠PAC=30°，得出∠C=∠PAC，即可证出AP=PC．
解答：证明：∵AB=AC，∠BAC=120°，
∴∠B=∠C=30°，
∵PA⊥AB，
∴∠BAP=90°，
∴∠PAC=∠BAC-∠BAP=30°，
∴∠C=∠PAC，
∴AP=PC．
∴∠B=∠C=30°，
∵PA⊥AB，
∴∠BAP=90°，
∴∠PAC=∠BAC-∠BAP=30°，
∴∠C=∠PAC，
∴AP=PC．
点评：本题考查了等腰三角形的性质以及垂直的定义；弄清角之间的关系求出∠C=∠PAC是解题的关键．
练习册系列答案
相关题目
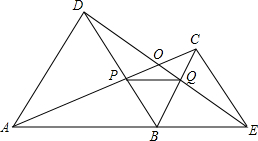已知△ABD和△BCE均为等边三角形，连接AC，DE交DB于点P，交DE于点O，你能得到哪些结论，并给予证明．
如图，线段AB=10cm，点C为线段A上一点，BC=3cm，点D，E分别为AC和AB的中点，求线段DE的长．
如图，点O在直线BC上，∠1与∠2互余，OE平分∠AOC，∠1=27°20′．求∠2，∠3的度数．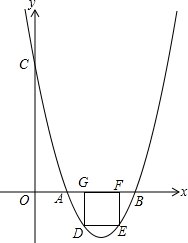
如图4，已知抛物线y=ax2+bx+c（a＞0）经过点A（2，0），B（6，0），交y轴于点C，且S△ABC=16．
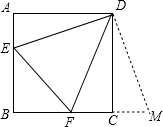正方形ABCD的边长为6，E，F分别是AB，BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．