题目内容
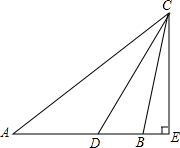 如图,△ABC中,AB=BC,CD平分∠ACB,CE⊥AB于E,若∠DCE=30°,求△ABC各角的度数.
如图,△ABC中,AB=BC,CD平分∠ACB,CE⊥AB于E,若∠DCE=30°,求△ABC各角的度数.考点:等腰三角形的性质
专题:
分析:先根据三角形的内角和定理求出∠CDE=60°,再利用等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠ACD=20°,∠BAC=∠ACB=40°,根据三角形的内角和定理求出∠ABC的度数.
解答:解:∵CE⊥AB,∠DCE=30°,
∴∠CDE=60°,
∵AB=BC,
∴∠BAC=∠ACB,
∵CD平分∠ACB,
∴∠ACD=
∠ACB,
∵∠CDE=∠BAC+∠ACD,
∴∠ACD=20°,∠BAC=∠ACB=40°,
∴∠ABC=100°.
故△ABC中,∠BAC的度数是40°,∠ACB的度数40°,∠ABC的度数100°.
∴∠CDE=60°,
∵AB=BC,
∴∠BAC=∠ACB,
∵CD平分∠ACB,
∴∠ACD=
| 1 |
| 2 |
∵∠CDE=∠BAC+∠ACD,
∴∠ACD=20°,∠BAC=∠ACB=40°,
∴∠ABC=100°.
故△ABC中,∠BAC的度数是40°,∠ACB的度数40°,∠ABC的度数100°.
点评:本题考查等腰三角形的性质、三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.

练习册系列答案
相关题目
 如图,线段AB=10cm,点C为线段A上一点,BC=3cm,点D,E分别为AC和AB的中点,求线段DE的长.
如图,线段AB=10cm,点C为线段A上一点,BC=3cm,点D,E分别为AC和AB的中点,求线段DE的长.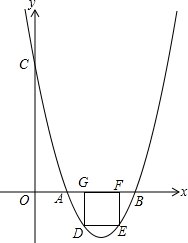 如图4,已知抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),交y轴于点C,且S△ABC=16.
如图4,已知抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),交y轴于点C,且S△ABC=16.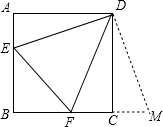 正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM. 如图,已知四个点A、B、C、D,根据下列要求画图:
如图,已知四个点A、B、C、D,根据下列要求画图: 已知:如图,A,B,C在同一条线段上,M是线段AC的中点,N是线段BC的中点,且AM=5cm,CN=3cm,则线段AB的长为
已知:如图,A,B,C在同一条线段上,M是线段AC的中点,N是线段BC的中点,且AM=5cm,CN=3cm,则线段AB的长为 如图,△ABC中,∠ACB=90°,CD是高,若∠A=30°,BD=1,则AD=
如图,△ABC中,∠ACB=90°,CD是高,若∠A=30°,BD=1,则AD=