题目内容
 如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )
如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )| A、12 | B、4 | C、8 | D、不确定 |
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:根据角平分线的定义可得∠ABE=∠CBE,∠ACE=∠BCE,再根据两直线平行,内错角相等可得∠CBE=∠BEM,∠BCE=∠CEN,然后求出∠ABE=∠BEM,∠ACE=∠CEN,根据等角对等边可得BM=ME,CN=NE,然后求出△AMN的周长=AB+AC.
解答:解:∵∠ABC和∠ACB的平分线交于点E,
∴∠ABE=∠CBE,∠ACE=∠BCE,
∵MN∥BC,
∴∠CBE=∠BEM,∠BCE=∠CEN,
∴∠ABE=∠BEM,∠ACE=∠CEN,
∴BM=ME,CN=NE,
∴△AMN的周长=AM+ME+AN+NE=AB+AC,
∵AB=AC=4,
∴△AMN的周长=4+4=8.
故选C.
∴∠ABE=∠CBE,∠ACE=∠BCE,
∵MN∥BC,
∴∠CBE=∠BEM,∠BCE=∠CEN,
∴∠ABE=∠BEM,∠ACE=∠CEN,
∴BM=ME,CN=NE,
∴△AMN的周长=AM+ME+AN+NE=AB+AC,
∵AB=AC=4,
∴△AMN的周长=4+4=8.
故选C.
点评:本题考查了等腰三角形的判定与性质,平行线的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、异号两数相加,取较大的符号,并把绝对值相加 |
| B、同号两数相减,取相同的符号,并把绝对值相减 |
| C、符号相反的两个数相加得0 |
| D、0加上一个数仍得这个数 |
 如图,在△ABC中有矩形DGFE,点G,F在BC上,点D,E分别在AB,AC上,AH⊥BC交DE于点M.若DG:DE=2:3,BC=15cm,AH=10cm,求矩形DGFE各边的长.
如图,在△ABC中有矩形DGFE,点G,F在BC上,点D,E分别在AB,AC上,AH⊥BC交DE于点M.若DG:DE=2:3,BC=15cm,AH=10cm,求矩形DGFE各边的长.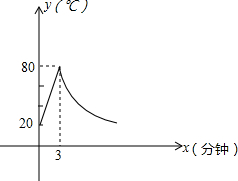 制作一种模型,需要先将材料加热,待其充分融合后,再进行操作.该材料的温度为y(℃),从加热开始计算的时间为x(分钟).该材料加热时,温度y与x成一次函数关系,停止加热后,温度y与x成反比例函数关系.如图,已知该材料在加热前的温度为20℃,加热3分钟后温度达到80℃.
制作一种模型,需要先将材料加热,待其充分融合后,再进行操作.该材料的温度为y(℃),从加热开始计算的时间为x(分钟).该材料加热时,温度y与x成一次函数关系,停止加热后,温度y与x成反比例函数关系.如图,已知该材料在加热前的温度为20℃,加热3分钟后温度达到80℃.