题目内容
10.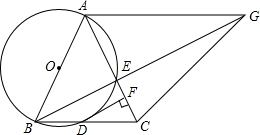 如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC,垂足为F.
如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC,垂足为F.(1)求证:DF为⊙O的切线;
(2)若过点A且与BC平行的直线交BE延长线于点G,连接CG,设⊙O半径为5.
①当CF=$\frac{5}{2}$时,四边形ABCG是菱形;
②当BC=4$\sqrt{5}$时,四边形ABCG的面积是100.
分析 (1)连结AD,OD,根据直径所对的圆周角为直角得到∠ADB=90°,再根据等腰三角形的性质得BD=DC,则OD为△ABC的中位线,所以OD∥AC,而DF⊥AC,
则DF⊥OD,所以可判断DF是⊙O的切线;
(2)①根据等腰三角形的性质得到BD=DC,根据菱形的性质得到,AD=BC,推出△ABC是等边三角形,根据等边三角形的性质得到CD=$\frac{1}{2}$BC=$\frac{1}{2}$AB=5,∠ACB=60°,根据直角三角形的性质得到CF=$\frac{1}{2}$CD=$\frac{5}{2}$,即可得到结论;
②根据等腰三角形的性质得到BD=$\frac{1}{2}$BC=2$\sqrt{5}$,根据勾股定理得到AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=4$\sqrt{5}$,根据圆周角定理得到∠AEB=∠ADB=90°,推出△ACD∽△BCE,根据相似三角形的性质列方程得到CE=4,BE=8,再通过△AGE∽△BCE,得到EG=12,于是得到结论.
解答 (1)证明:连结AD,OD,如图,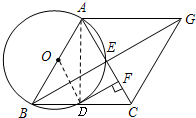 ∵AB是⊙O的直径,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵△ABC是等腰三角形,
∴BD=DC,
又∵AO=BO,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)解:①∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵△ABC是等腰三角形,
∴BD=DC,
又∵AO=BO=$\frac{1}{2}$AB=5,
∴AB=10,
若四边形ABCG是菱形,
则AD=BC,
∴△ABC是等边三角形,
∴CD=$\frac{1}{2}$BC=$\frac{1}{2}$AB=5,∠ACB=60°,
∵DF⊥AC,
∴CF=$\frac{1}{2}$CD=$\frac{5}{2}$,
∴当CF=$\frac{5}{2}$时,四边形ABCG是菱形;
故答案为:$\frac{5}{2}$;
②∵AB=AC,AD⊥BC,
∴BD=$\frac{1}{2}$BC=2$\sqrt{5}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=4$\sqrt{5}$,
∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°,
∴∠ADC=90°,
∵∠ACB=∠ACB,
∴△ACD∽△BCE,
∴$\frac{AC}{BC}=\frac{CD}{CE}$=$\frac{AD}{BE}$,即$\frac{10}{4\sqrt{5}}=\frac{2\sqrt{5}}{CE}$=$\frac{4\sqrt{5}}{BE}$,
∴CE=4,BE=8,
∴AE=AC-CE=6,
∵AG∥BC,
∴△AGE∽△BCE,
∴$\frac{AE}{CE}=\frac{GE}{BE}$,即$\frac{6}{4}=\frac{EG}{8}$,
∴EG=12,
∴四边形ABCG的面积=S△ABC+S△ACG=$\frac{1}{2}$×4$\sqrt{5}$×4$\sqrt{5}$+$\frac{1}{2}$×10×12=100.
故答案为:100.
点评 本题考查了切线的判定定理,相似三角形的判定和性质,等腰三角形的性质,等边三角形的判定和性质,菱形的性质,勾股定理,证得△ACD∽△BCE是解答(3)小题的关键.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
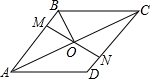 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )| A. | 28° | B. | 52° | C. | 62° | D. | 72° |
| A. | AB⊥BC | B. | AC⊥BD | C. | AB=BC | D. | AC=BD |
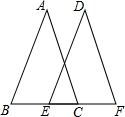 如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )
如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )