Question

20．已知菱形的周长为40，两对角线比为3：4，则两对角线的长分别为12，16．

Answer 1

分析 首先根据题意画出图形，然后设OA=3x，OB=4x，由菱形的性质，可得方程：10²=（3x）²+（4x）²，继而求得答案．

解答 解：如图，∵菱形的周长为40，
∴AB=10，OA=$\frac{1}{2}$AC，OB=$\frac{1}{2}$BD，AC⊥BD，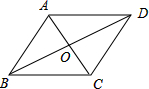
∵两条对角线长度之比为3：4，
∴OA：OB=3：4，
设OA=3x，OB=4x，
在Rt△AOB中，AB²=OA²+OB²，
∴10²=（3x）²+（4x）²，
解得：x=2，
∴OA=6，OB=8，
∴AC=12，BD=16，
∴对角线的长度分别为：12，16．
故答案为：12，16．

点评 此题考查了菱形的性质以及勾股定理．此题难度适中，注意掌握数形结合思想与方程思想的应用．