题目内容
已知二次函数y=ax2+bx+c中函数y与自变量x之间的部分对应值如下表所示，点A（x1，y1）、B（x2，y2）在函数图象上，当0＜x1＜1，2＜x2＜3时，则y1 y2（填“＞”或“＜”）．
x … 0 1 2 3 …
y … 1 ﹣2 ﹣3 ﹣2 …
＞
考点： 二次函数图象上点的坐标特征．
专题： 数形结合．
分析： 利用表中数据得到抛物线开口向上，对称轴为直线x=2，然后利用抛物线开口向上时，离对称轴越远的点所对应的函数值越大进行求解．
解答： 解：根据表中数据得到抛物线开口向上，对称轴为直线x=2，
因为0＜x1＜1，2＜x2＜3，
所以点A比点B离对称轴要远，
所以y1＞y2．
故答案为＞．
点评： 本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
练习册系列答案
阅读快车系列答案
相关题目
C．
D．2
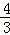x2+bx+c与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．
