题目内容
如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l的异侧，若∠AMB=45°，则四边形MANB面积的最大值是．
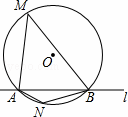
4
解：过点O作OC⊥AB于C，交⊙O于D、E两点，连结OA、OB、DA、DB、EA、EB，如图，
∵∠AMB=45°，
∴∠AOB=2∠AMB=90°，
∴△OAB为等腰直角三角形，
∴AB=OA=2，
∵S四边形MANB=S△MAB+S△NAB，
∴当M点到AB的距离最大，△MAB的面积最大；当N点到AB的距离最大时，△NAB的面积最大，
即M点运动到D点，N点运动到E点，
此时四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB=
AB•CD+AB•CE=AB（CD+CE）=AB•DE=×2
×4=4．
故答案为：4．
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
是互为相反数，且关于x的方程kx
2+ax+b=0有两个不相等的实数根，求k的取值范围．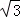
，将△ABC绕点P旋转180°，得到△MCB．
