题目内容
12．
如图，已知∠AOB=60°，点P在边OA上，OP=16，点M，N在边OB上，PM=PN，若MN=4，则OM=（ ）| A． | 6 | B． | 5 | C． | 4 | D． | 3 |
分析 首先过点P作PD⊥OB于点D，利用直角三角形中30°所对边等于斜边的一半得出DO的长，再利用等腰三角形的性质求出OM的长．
解答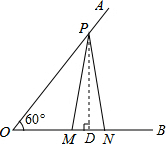 
解：过点P作PD⊥OB于点D，
∵∠AOB=60°，PD⊥OB，OP=16，
∴DO=8，
∵PM=PN，MN=4，PD⊥OB，
∴MD=ND=2，
∴MO=6．
故选A
点评 此题主要考查了直角三角形中30°所对边等于斜边的一半得出DO的长以及等腰三角形的性质，得出OD的长是解题关键．
练习册系列答案
相关题目
1．旺都超市进了一批货物，出售时要在进价的基础上加上一定利润，其数量x（千克）与售价y（元）之间的关系如表：
（1）用含x的式子表示y，得y=4.2x；
（2）计算当售价y=33.6时，货物的数量是多少？
| 数量x千克 | 售价y元 |
| 1 | 4+0.2 |
| 2 | 8+0.4 |
| 3 | 12+0.6 |
| 4 | 16+0.8 |
| 5 | 20+1 |
| … | … |
（2）计算当售价y=33.6时，货物的数量是多少？
某商店试销一款运动服，经市场调，发现平均日销量y（件）是销售单价x（元/件）的一次函数，其图象如图所示．