题目内容
 如图,在5×5的方格纸中,小正方形的面积为1,小正方形的顶点为格点,请你在图中选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连结后围成的图形面积尽可能大,并求出这个最大面积.
如图,在5×5的方格纸中,小正方形的面积为1,小正方形的顶点为格点,请你在图中选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连结后围成的图形面积尽可能大,并求出这个最大面积.考点:作图—应用与设计作图,三角形的面积
专题:网格型
分析:这是一个5×5的方格纸,共有25个格点.现在要围成一个面积最大的图形,根据格点面积公式,要使图形面积最大,必须使图形包含的内部格点数和周界上格点数尽可能多.由方格纸可知,内部格点数最多为4×4=16,周界上格点数最多为5×4=20.但是,当周界上格点数为最多时,不符合题中“任意3个格点不在一条直线上”的条件,因此,适当调整图上7个格点的位置,如下图所示,就得到了面积最大的图形.
解答:解:7个格点分布如下图:

所围成图形的最大面积为:5×5-0.5×3=23.5(平方厘米).

所围成图形的最大面积为:5×5-0.5×3=23.5(平方厘米).
点评:本题考查了作图-应用与设计作图,解题的关键是分析题干,根据题意和图形特点作出格点分布位置,然后计算面积.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
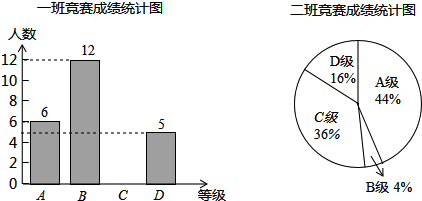
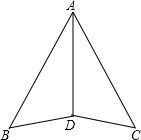 如图,∠B=∠C,AD平分∠BAC,求证:△ABD≌△ACD.若BD=3cm,则CD有多长?
如图,∠B=∠C,AD平分∠BAC,求证:△ABD≌△ACD.若BD=3cm,则CD有多长?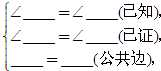
 如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.
如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.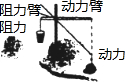 一杠杆装置如图,杆的一端拉起一物体,所受重力为300N.物体对杆的拉力的作用点到支点的杠长为1m.杠与水平线的倾斜角为45°,设在杠的另一端施加的压力为F(N),压力作用点到支点的距离为d(m)(杠杆自身的重量忽略不计).
一杠杆装置如图,杆的一端拉起一物体,所受重力为300N.物体对杆的拉力的作用点到支点的杠长为1m.杠与水平线的倾斜角为45°,设在杠的另一端施加的压力为F(N),压力作用点到支点的距离为d(m)(杠杆自身的重量忽略不计). 如图,在△ABC中,已知∠BAC=45°,AD⊥BC于点D,BD=2,DC=3,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题:
如图,在△ABC中,已知∠BAC=45°,AD⊥BC于点D,BD=2,DC=3,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题: 如图,已知点D,E,F分别是△ABC的三边的中点.
如图,已知点D,E,F分别是△ABC的三边的中点.