题目内容
 如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.
如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.(1)图中有哪些三角形相似?
(2)若AD=4,BE=2,求DE的长.
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:(1)根据正方形的性质和相似三角形的判定方法可知由6对三角形相似;
(2)由(1)中的三角形相似看可得到关于正方形边长的比例式,代入数值计算即可.
(2)由(1)中的三角形相似看可得到关于正方形边长的比例式,代入数值计算即可.
解答:解:(1)△CGF∽△CAB∽△DAG∽△EFB;
(2)∵四边形GDEF是正方形,
∴GD=DE=EF,
∵△ADG∽△FEB,
∴AD:EF=DG:BE,
∵AD=4,BE=2,
∴4:EF=DG:2,
∴4:DE=DE:2,
∴DE=2
.
(2)∵四边形GDEF是正方形,
∴GD=DE=EF,
∵△ADG∽△FEB,
∴AD:EF=DG:BE,
∵AD=4,BE=2,
∴4:EF=DG:2,
∴4:DE=DE:2,
∴DE=2
| 2 |
点评:本题考查了正方形的性质、相似三角形的判定和性质,解题的关键是注意图形中的相等线段的替换.

练习册系列答案
相关题目
 如图,两块相同的直角三角板拼成一个图形.
如图,两块相同的直角三角板拼成一个图形.
 如图,在5×5的方格纸中,小正方形的面积为1,小正方形的顶点为格点,请你在图中选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连结后围成的图形面积尽可能大,并求出这个最大面积.
如图,在5×5的方格纸中,小正方形的面积为1,小正方形的顶点为格点,请你在图中选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连结后围成的图形面积尽可能大,并求出这个最大面积.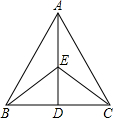 已知:如图,D是△ABC中BC边上一点,EB=EC,∠ABE=∠ACE,求证:AB=AC.
已知:如图,D是△ABC中BC边上一点,EB=EC,∠ABE=∠ACE,求证:AB=AC. 如图,平行四边形ABCD的对角线AC,BD相交于点O,一直线绕点O旋转与AD,BC分别交于E,F.
如图,平行四边形ABCD的对角线AC,BD相交于点O,一直线绕点O旋转与AD,BC分别交于E,F.