题目内容
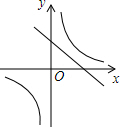
18.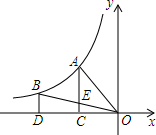 如图是反比例函数y=-$\frac{4}{x}$(x<0)的图象的一支.
如图是反比例函数y=-$\frac{4}{x}$(x<0)的图象的一支.(1)写出图象的另一支在哪个象限;
(2)若点A1(a1,b1),点A2(a2,b2),点A3(a3,b3)是该图象上的三点,且a1<a2<a3,比较b1,b2,b3的大小;
(3)若点A(-2,m),B(-4,n)是该图象上的两点,过点A,B两点作AC⊥x轴,BD⊥x轴,垂足分别是点C,D,连接OA,OB,设OB交AC于点E,求△OEC的面积.
分析 (1)根据反比例函数的系数为-4即可得出结论;
(2)根据反比例函数的增减性即可得出结论;
(3)先求出mn的值,再利用待定系数法求出E点坐标,根据三角形的面积公式即可得出结论.
解答 解:(1)∵反比例函数y=-$\frac{4}{x}$中,k=-4<0,
∴此函数的图象分别位于二四象限,
∴图象的另一支在第四象限;
(2)∵函数图象在第四象限是增函数,
∴b1<b2<b3;
(3)∵点A(-2,m),B(-4,n)是该图象上的两点,
∴m=-$\frac{4}{-2}$=2,n=-$\frac{4}{-4}$=1,
∴A(-2,2),B(-4,1).
设直线OB的解析式为y=kx(k≠0),
∵B(-4,1),
∴1=-4k,解得k=-$\frac{1}{4}$,
∴直线OB的解析式为y=-$\frac{1}{4}$x,
∴E(-2,$\frac{1}{2}$),
∴S△OEC=$\frac{1}{2}$×2×$\frac{1}{2}$=$\frac{1}{2}$.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
8.将一次函数y=$\frac{1}{2}$x的图象向左平移4个单位,平移后,若y>0,则x的取值范围是( )
| A. | x>4 | B. | x>-4 | C. | x>2 | D. | x>-2 |

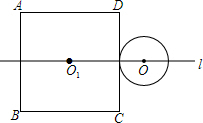 如图,正方形边长为4,⊙O的半径为1,正方形中心O1与圆心O在直线l上,⊙O与CD边相切,⊙O以1cm/s的速度向左边运动.
如图,正方形边长为4,⊙O的半径为1,正方形中心O1与圆心O在直线l上,⊙O与CD边相切,⊙O以1cm/s的速度向左边运动.