题目内容
1.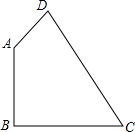 在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,则∠DAB的度数为( )
在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,则∠DAB的度数为( )| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
分析 连接AC,由已知可得AB=BC,从而可求得∠BAC的度数,再根据已知可求得AC:CD:DA=2$\sqrt{2}$:3:1,从而发现其符合勾股定理的逆定理,即可得到∠DAC=90°,从而不难求得∠DAB的度数.
解答  解:如图,连接AC,
解:如图,连接AC,
∵AB:BC:CD:DA=2:2:3:1,且∠ABC=90°,
∴AB=BC,
∴∠BAC=∠ACB=45°,
∴AB:BC:AC=2:2:2$\sqrt{2}$=1:1:$\sqrt{2}$,
∴AC:CD:DA=2$\sqrt{2}$:3:1,
∵AC2+AD2=CD2,
∴∠DAC=90°,
∴∠DAB=45°+90°=135°.
故选C.
点评 本题考查了等腰三角形的性质、勾股定理、勾股定理的逆定理.解题的关键是连接AC,并证明△ACD是直角三角形.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | 2,3,$\sqrt{13}$是一组勾股数 | |
| B. | 估算得$\sqrt{5}$$<\root{3}{7}$ | |
| C. | 无理数是无限小数 | |
| D. | 在海面上知道一个方位角就可以确定一个目标的位置 |
 如图,∠A=90°,E为BC上的一点,A点和E点关于BD的对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
如图,∠A=90°,E为BC上的一点,A点和E点关于BD的对称,B点、C点关于DE对称,求∠ABC和∠C的度数. 如图,已知点A(m,n)、点B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,∠OAB=90°,AO=AB,求$\frac{m}{n}$的值.
如图,已知点A(m,n)、点B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,∠OAB=90°,AO=AB,求$\frac{m}{n}$的值. 如图所示是某工厂的大门,它是由一个正方形和一个半圆组成的,正方形的边长为5米,一辆装货的卡车宽为4米,高为6米,则这辆卡车能否通过此大门?说明理由.
如图所示是某工厂的大门,它是由一个正方形和一个半圆组成的,正方形的边长为5米,一辆装货的卡车宽为4米,高为6米,则这辆卡车能否通过此大门?说明理由.
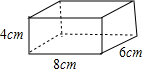 如图所示的是一个长8cm,宽6cm,高4cm的长方体,现在把它等分为24个棱长为2cm的小正方体
如图所示的是一个长8cm,宽6cm,高4cm的长方体,现在把它等分为24个棱长为2cm的小正方体