题目内容
17.用平方法比较$\sqrt{6}$$+\sqrt{11}$与$\sqrt{14}$$+\sqrt{3}$的大小.分析 先计算两个数的平方,再根据平方法的比较原理进行判断即可.
解答 解:$(\sqrt{6}+\sqrt{11})^{2}$=17+2$\sqrt{66}$,
$(\sqrt{14}+\sqrt{3})^{2}$=17+$\sqrt{42}$,
∵17+2$\sqrt{66}$>17+$\sqrt{42}$>1,
∴$(\sqrt{6}+\sqrt{11})^{2}$>$(\sqrt{14}+\sqrt{3})^{2}$
∴$\sqrt{6}+\sqrt{11}>\sqrt{14}+\sqrt{3}$
点评 此题主要考查运用平方法比较二次根式,知道平方法的比较原理(当数大于1时,平方越大,数越大;当数大于0且小于1时,平方越大,数越小)并会计算二次根式的平方是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
5.已知$\frac{1}{a}$-$\frac{1}{b}$=2,则$\frac{ab}{2a+3ab-2b}$的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 1 | D. | -1 |
9.计算100x•100y+1的结果是( )
| A. | 100x+y+1 | B. | 102x+y+3 | C. | 102x+2y+3 | D. | 102x+2y+2 |
16. 一次函数,y=kx+b(k、b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是( )
一次函数,y=kx+b(k、b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是( )
 一次函数,y=kx+b(k、b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是( )
一次函数,y=kx+b(k、b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是( )| A. | x>-2 | B. | x>0 | C. | x<-2 | D. | x<0 |
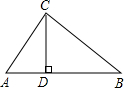 如图,在△ABC中,CD⊥AB于D,∠A=60°,∠B=45°,BC=4,
如图,在△ABC中,CD⊥AB于D,∠A=60°,∠B=45°,BC=4,