题目内容
12.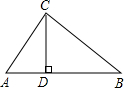 如图,在△ABC中,CD⊥AB于D,∠A=60°,∠B=45°,BC=4,
如图,在△ABC中,CD⊥AB于D,∠A=60°,∠B=45°,BC=4,(1)求CD的长;
(2)求AB的长.
分析 (1)在Rt△BCD中,由于∠B=45°,BC=4,则根据等腰三角形的性质得到CD=BD=2$\sqrt{2}$;
(2)在Rt△ADC中,根据含30度的直角三角形三边的关系得到AD=$\frac{2\sqrt{6}}{3}$,然后求AD+CD即可.
解答 解:(1)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
在Rt△BCD中,∠B=45°,BC=4,
∴CD=BD=$\frac{\sqrt{2}}{2}$BC=2$\sqrt{2}$,
(2)在Rt△ADC中,∠A=60°,CD=2$\sqrt{2}$,
∴AD=$\frac{\sqrt{3}}{3}$CD=$\frac{2\sqrt{6}}{3}$,
∴AB=AD+BD=$\frac{2\sqrt{6}}{3}$+2$\sqrt{2}$=$\frac{2\sqrt{6}+6\sqrt{2}}{3}$.
点评 本题考查了勾股定理,解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目
 表示(-4xyz)2,“方框”
表示(-4xyz)2,“方框” 表示-5abdc,求
表示-5abdc,求 ×
× 的值.
的值. 如图,已知抛物线与x交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).