题目内容
 如图,AB为⊙O的直径,弦CD⊥AB于点E,若AE=8,BE=2,则AC=
如图,AB为⊙O的直径,弦CD⊥AB于点E,若AE=8,BE=2,则AC=考点:勾股定理
专题:
分析:连接CO,根据勾股定理求出CE的长,再根据勾股定理求出AC的长即可.
解答:解:连接CO,
∵AB为⊙O的直径,弦CD⊥AB于点E,
∴CE=ED,
∵AE=8,BE=2,
∴AB=10,
∴CO=AO=5,OE=AE-AO=8-5=3,
∴CE=
=4,
AC=
=4
.
故答案为4
.

∵AB为⊙O的直径,弦CD⊥AB于点E,
∴CE=ED,
∵AE=8,BE=2,
∴AB=10,
∴CO=AO=5,OE=AE-AO=8-5=3,
∴CE=
| 52-32 |
AC=
| 42+82 |
| 5 |
故答案为4
| 5 |
点评:本题考查了勾股定理,由垂径定理得出CD⊥AB得到直角三角形是解题的关键.

练习册系列答案
相关题目
由二次函数y=2(x-3)2+1,可知( )
| A、其图象的开口向下 |
| B、其图象的对称轴为直线x=-3 |
| C、其最小值为1 |
| D、当x≤3时,y随x的增大而增大 |
下列方程中,关于x的一元二次方程是( )
| A、3(x+1)2=(2x+1) | ||
B、x+
| ||
| C、ax2+bx+c=0 | ||
| D、x2+2x=x2-1 |
 如图1,在△ABC中,∠C=90°,AD平分∠BAC,CD=5cm,则点D到AB边的距离是
如图1,在△ABC中,∠C=90°,AD平分∠BAC,CD=5cm,则点D到AB边的距离是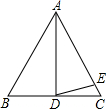 如图,在△ABC中,AB=AC,BD=CD,∠BAD=40°,且AD=AE,则∠EDC等于
如图,在△ABC中,AB=AC,BD=CD,∠BAD=40°,且AD=AE,则∠EDC等于