题目内容
5．
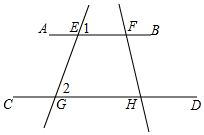如图，已知直线AB，CD，EG，FH分别相交于点E，G，H，F，且∠1=∠2，且∠AFH=115°，试求∠CHF的度数．
分析 先根据同位角相等，两直线平行，得出AB∥CD，再根据两直线平行，同旁内角互补，即可得到∠CHF的度数．
解答 解：∵∠1=∠2，
∴AB∥CD，
∴∠AFH+∠CHF=180°，
∵∠AFH=115°，
∴∠CHF=65°．
点评 本题主要考查了平行线的性质与判定的运用，解题时注意：平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
练习册系列答案
阅读快车系列答案
相关题目
16．在下列的方程中，解是x=1的方程是（ ）
| A． | 2x=x-1 | B． | 1-x=0 | C． | -2x=2 | D． | 4x-1=-3 |
13．若点A（-3，y）在第三象限，则点B（-3，-y）在（ ）
| A． | 第四象限 | B． | 第三象限 | C． | 第二象限 | D． | 第一象限 |
14．若m≠0，n≠0，m＞n，化简二次根式$\sqrt{-{m}^{3}n}$的结果是（ ）
| A． | -m$\sqrt{-mn}$ | B． | -m$\sqrt{mn}$ | C． | m$\sqrt{mn}$ | D． | m$\sqrt{-mn}$ |
