题目内容
17.已知α、β是关于x的一元二次方程的x2+(2m+3)x+m2=0两个不相等的实数根,且满足α+β+αβ=0,则m的值是3.分析 由方程有两个不相等的实数根,可得出△=12m+9>0,解之即可得出m的取值范围,由根与系数的关系结合α+β+αβ=0,可得出关于m的一元二次方程,解之即可得出m的值,再由m的取值范围可确定m的值.
解答 解:∵关于x的一元二次方程的x2+(2m+3)x+m2=0有两个不相等的实数根,
∴△=(2m+3)2-4m2=12m+9>0,
解得:m>-$\frac{3}{4}$.
∵α、β是关于方程x2+(2m+3)x+m2=0的两个实数根,
∴α+β=-(2m+3),αβ=m2.
∵α+β+αβ=0,
∴m2-2m-3=0,
解得:m1=-1,m2=3.
∵m>-$\frac{3}{4}$,
∴m=3.
故答案为:3.
点评 本题考查了根的判别式以及根与系数的关系,根据根与系数的关系结合α+β+αβ=0,列出关于m的一元二次方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一个袋中有2个红球,3个黄球和5个白球,这些球除颜色外完全相同,现在从中任意摸出一个球,则P(模到红球)等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{10}$ |
7.医学研究发现一种新病毒的直径约为0.000059毫米,则数0.000059用科学记数法表示为( )
| A. | 5.9×10-4 | B. | 5.9×10-5 | C. | 0.59×104 | D. | 0.59×105 |
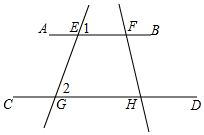 如图,已知直线AB,CD,EG,FH分别相交于点E,G,H,F,且∠1=∠2,且∠AFH=115°,试求∠CHF的度数.
如图,已知直线AB,CD,EG,FH分别相交于点E,G,H,F,且∠1=∠2,且∠AFH=115°,试求∠CHF的度数.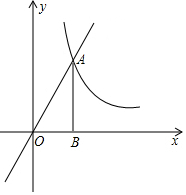 已知图中的曲线是反比例函数y=$\frac{m-5}{x}$(m为常数)图象的一支.
已知图中的曲线是反比例函数y=$\frac{m-5}{x}$(m为常数)图象的一支.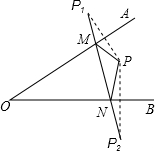 如图,∠AOB=30°,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,OP=18,图中线段之间相等的关系式有(至少写出两组)PM=P1M,PN=P2N;△PMN的周长为18.
如图,∠AOB=30°,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,OP=18,图中线段之间相等的关系式有(至少写出两组)PM=P1M,PN=P2N;△PMN的周长为18. 如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.
如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.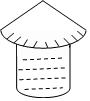 如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元,那么购买油毡所需要的费用是565.2元(结果保留一位小数).
如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元,那么购买油毡所需要的费用是565.2元(结果保留一位小数).