题目内容
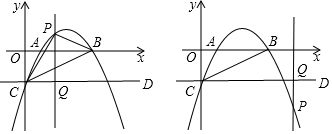
15.如图,抛物线y=ax2+$\frac{5}{2}$x-2与x轴相交于点A(1,0)与点B,与y轴相交于点C,直线CD∥x轴,在CD上有一动点Q,过点Q作平行线于y轴的直线PQ与抛物线交点为P,设点P的横坐标为t,连接CP、PB.(1)求抛物线的解析式;
(2)当1<t<4时,求△CBP面积的最大值;
(3)当t>4时,是否存在点P,使以C、P、Q为顶点的三角形与△AOC相似?若存在,求出此时点P的坐标;若不存在,请说明理由.
分析 (1)将x=1代入抛物线的解析式求得a的值即可;
(2)如图1所示:先求得A(1,0),B(4,0)、C(0,-2),然后求得BC的解析式,设点P的坐标为(t,-$\frac{1}{2}$t2+$\frac{5}{2}$t-2),则点E(t,$\frac{1}{2}$t-2).则PE=-$\frac{1}{2}$t2+2t,然后列出△CBP的面积与t的函数关系式,最后利用配方法求解即可;
(3)由题意可知tan∠OCA=$\frac{1}{2}$,则∠PCQ=$\frac{1}{2}$或∠PCQ=2,设点Q的坐标为(t,-2),则点P的坐标为(t,-$\frac{1}{2}$t2+$\frac{5}{2}$t-2)则CQ=t,PQ=|-$\frac{1}{2}$t2+$\frac{5}{2}$t,然后依据锐角三角函数的定义列方程求解即可.
解答 解:(1)将x=1代入得:a+$\frac{5}{2}$-2=0,解得:a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2.
(2)如图1所示:
令y=0得:-$\frac{1}{2}$x2+$\frac{5}{2}$x-2=0,解得:x=1或x=4,
∴点A(1,0),B(4,0).
当x=0时,y=-2,
∴C(0,-2).
设直线BC的解析式为y=kx-2,将点B的坐标代入得:4k-2=0,解得:k=$\frac{1}{2}$.
设直线BC的解析式为y=$\frac{1}{2}$x-2.
设点P的坐标为(t,-$\frac{1}{2}$t2+$\frac{5}{2}$t-2),则点E(t,$\frac{1}{2}$t-2).则PE=-$\frac{1}{2}$t2+$\frac{5}{2}$t-2-$\frac{1}{2}$t+2=-$\frac{1}{2}$t2+2t.
∴△CBP的面积=$\frac{1}{2}$OB•PE=$\frac{1}{2}$×4×(-$\frac{1}{2}$t2+2t)=-t2+4t-4+4=-(t-2)2+4,
∴当t=2时,△CBP的面积最大,最大值为4.
(3)∵AO=1,OC=2,
∴tan∠OCA=$\frac{1}{2}$.
∵C、P、Q为顶点的三角形与△AOC相似,
∴∠PCQ=$\frac{1}{2}$或∠PCQ=2.
设点Q的坐标为(t,-2),则点P的坐标为(t,-$\frac{1}{2}$t2+$\frac{5}{2}$t-2).
∴CQ=t,PQ=|-$\frac{1}{2}$t2+$\frac{5}{2}$t|.
∴$\frac{|-\frac{1}{2}{t}^{2}+\frac{5}{2}t|}{t}$|=2或$\frac{|-\frac{1}{2}{t}^{2}+\frac{5}{2}t|}{t}$|=$\frac{1}{2}$.
解得t=1或t=9或t=4或t=6.
∵t>4,
∴t=6或t=9.
∴点P的坐标为(6,-5)或(9,-20).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数、一次函数的解析式、相似三角形的性质、二次函数的最值,列出△BCP的面积与t的函数关系式是解答问题(2)的关键,依据相似三角形的对应边之比为定值列出关于t的方程是解答问题(3)的关键.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案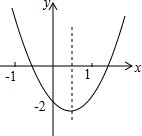 二次函数y=ax2+bx+c的图象如图所示,则下列结论:①abc<0;②b2-4ac>0;③2a+b>0;④a+b+c<0;⑤ax2+bx+c+2=0的解为x=0,其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论:①abc<0;②b2-4ac>0;③2a+b>0;④a+b+c<0;⑤ax2+bx+c+2=0的解为x=0,其中正确的有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
| A. | 5.9×10-4 | B. | 5.9×10-5 | C. | 0.59×104 | D. | 0.59×105 |
| A. | 3 | B. | 3$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 12 |
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
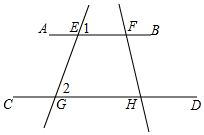 如图,已知直线AB,CD,EG,FH分别相交于点E,G,H,F,且∠1=∠2,且∠AFH=115°,试求∠CHF的度数.
如图,已知直线AB,CD,EG,FH分别相交于点E,G,H,F,且∠1=∠2,且∠AFH=115°,试求∠CHF的度数.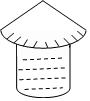 如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元,那么购买油毡所需要的费用是565.2元(结果保留一位小数).
如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元,那么购买油毡所需要的费用是565.2元(结果保留一位小数). 如图,△ABC三边的中线AD,BE,CF交于点G,若S△ABC=12,则图中阴影部分面积是( )
如图,△ABC三边的中线AD,BE,CF交于点G,若S△ABC=12,则图中阴影部分面积是( )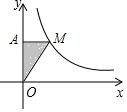 如图,M为反比例函数y=$\frac{k}{x}$的图象上的一点,MA垂直于y轴,垂足为A,△MAO的面积为4,则k的值为8.
如图,M为反比例函数y=$\frac{k}{x}$的图象上的一点,MA垂直于y轴,垂足为A,△MAO的面积为4,则k的值为8.