题目内容
6.已知Q是圆内接四边形ABCD的对角线的交点,PB、PD是圆的切线,且P在直线AC上,求证:(1)$\frac{QA}{OC}$=$\frac{AB•AD}{CB•CD}$;(2)$\frac{QA}{QC}$=$\frac{PA}{PC}$.分析 (1)根据相似三角形的判定方法得出△AQB∽△DQC以及△AQD∽△BQC,进而利用相似三角形的性质得出答案;
(2)根据相似三角形的判定方法得出△PAD∽△PBC以及△PAB∽△PBC,进而利用相似三角形的性质得出答案.
解答 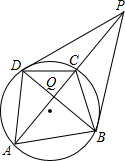 证明:(1)如图所示:
证明:(1)如图所示:
∵Q是圆内接四边形ABCD对角线的交点,∠ABQ=∠DCQ,
∠AQB=∠DQC,
∴△AQB∽△DQC,
∴$\frac{AB}{CD}$=$\frac{QA}{DQ}$①,
同理可得:△AQD∽△BQC,
∴$\frac{AD}{BC}$=$\frac{DQ}{QC}$②,
由①×②得:
$\frac{AB}{CD}$×$\frac{AD}{BC}$=$\frac{QA}{DQ}$×$\frac{DQ}{QC}$,
∴$\frac{QA}{QC}$=$\frac{AB•AD}{BC•DC}$;
(2)如图所示:∵PB、PD是圆的切线,
∴PB=PD,∠PDA=∠PCD,
∵∠DPA=∠CPD,
∴△PAD∽△PBC,
∴$\frac{PD}{PC}$=$\frac{AD}{DC}$③,
同理可得:△PAB∽△PBC,
∴$\frac{PA}{PB}$=$\frac{AB}{BC}$④,
∴由③×④得:$\frac{PD}{PC}$×$\frac{PA}{PB}$=$\frac{AD}{DC}$×$\frac{AB}{BC}$,
∴$\frac{PA}{PC}$=$\frac{AB•AD}{BC•CD}$,
由(1)得:$\frac{QA}{QC}$=$\frac{PA}{PC}$.
点评 此题主要考查了相似三角形的判定与性质以及切线的性质等知识,正确掌握相似三角形的判定与性质是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
11.-$\frac{2}{3}$的相反数是( )
| A. | -$\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
18. 如图,数轴上有A,B,C,D四个点,其中表示-2的相反数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示-2的相反数的点是( )
 如图,数轴上有A,B,C,D四个点,其中表示-2的相反数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示-2的相反数的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
15.下列计算中,不正确的是( )
| A. | (-2x2y)3=-6x6y3 | B. | -2x+3x=x | C. | 6xy2÷2xy=3y | D. | 2xy2•(-x)=-2x2y2 |
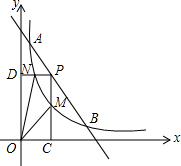 如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是$\frac{25}{2}$.
如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是$\frac{25}{2}$.