题目内容
18.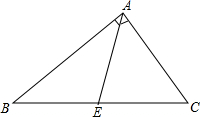 如图,已知AE是△ABC的中线,AB=8cm,AC=6cm,∠CAB=90°.
如图,已知AE是△ABC的中线,AB=8cm,AC=6cm,∠CAB=90°.(1)求△ABE的面积;
(2)求△ABE和△ACE的周长之差;
(3)若BC=10cm,求BC边上的高AD的长度.
分析 (1)由△AEC与△ABE是等底同高的两个三角形,它们的面积相等;
(2)由于AE是中线,那么BE=CE,于是△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE),化简可得△ACE的周长-△ABE的周长=AC-AB,易求其值(3)利用“面积法”来求线段AD的长度.
解答 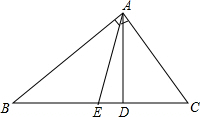 解:(1)如图,∵△ABC是直角三角形,∠BAC=90°,AB=8cm,AC=86m,
解:(1)如图,∵△ABC是直角三角形,∠BAC=90°,AB=8cm,AC=86m,
∴S△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}$×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴$\frac{1}{2}$BE•AD=$\frac{1}{2}$EC•AD,即S△ABE=S△AEC,
∴S△ABE=$\frac{1}{2}$S△ABC=12(cm2).
∴△ABE的面积是12cm2;
(2)∵AE为BC边上的中线,
∴BE=CE,
∴△ABE的周长-△ACE的周长=AB+AE+BE-(AC+CE+AE)=AB-AC=8-6=2(cm),
即△ACE和△ABE的周长的差是2cm;
(3)∵∠BAC=90°,AD是边BC上的高,
∴$\frac{1}{2}$AB•AC=$\frac{1}{2}$BC•AD,
∴AD=$\frac{AB•AC}{BC}$=$\frac{6×8}{10}$=4.8(cm),即AD的长度为4.8cm;
点评 本题考查了中线的定义、三角形周长的计算.解题的关键是利用三角形面积的两个表达式相等,求出AD.

练习册系列答案
相关题目
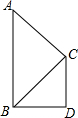 如图,△ABC∽△CBD,∠ACB=Rt∠,AB=8cm,BD=4cm,求BC,CD的长.
如图,△ABC∽△CBD,∠ACB=Rt∠,AB=8cm,BD=4cm,求BC,CD的长.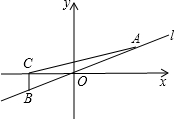 如图,点A(3,1)在直线l上.
如图,点A(3,1)在直线l上.