题目内容
12.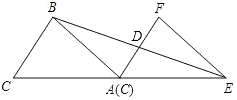 如图,在△ABC中,AB=AC,将△ABC沿射线CA方向平移,平移后顶点C到达点A处,得到△EFA.
如图,在△ABC中,AB=AC,将△ABC沿射线CA方向平移,平移后顶点C到达点A处,得到△EFA.(1)若平移过程中△ABC扫过的图形面积是9,求△ABC的面积;
(2)连接BE交AF于点D,试说明BE⊥AF于点D.
分析 (1)根据平移的性质得到AE=BF=AC,BF∥CE,△EFA≌△ABC,利用平行四边形的判定方法可得到四边形AEFB是平行四边形,则S△AEF=S△ABF=S△ABC,然后利用四边形BCEF的面积=3S△ABC进行计算;
(2)由于AB=AC,而AE=AC,则AB=AE,利用(1)中证得的四边形AEFB是平行四边形,根据菱形的判定方法有四边形AEFB是菱形,然后根据菱形的性质得到AF与BE互相垂直平分即可求解.
解答  解:(1)连结BF,
解:(1)连结BF,
∵将△ABC沿CA的方向平移CA的长,得△EFA,
∴AE=BF=AC,BF∥CE,△EFA≌△ABC,
∴四边形AEFB是平行四边形,
∴S△AEF=S△ABF=S△ABC,
∵△ABC扫过的图形面积是9,
∴△ABC的面积=3;
(2)AF与BE互相垂直平分.理由如下:
∵AB=AC,
而AE=AC,
∴AB=AE,
∵四边形AEFB是平行四边形,
∴四边形AEFB是菱形,
∴BE⊥AF于点D.
点评 本题考查了菱形的判定与性质:四边相等的四边形为菱形;邻边相等的平行四边形为菱形;菱形的对角线互相垂直平分,且对角线平分对角.也考查了平行四边形的判定与性质以及平移的性质.

练习册系列答案
相关题目
2.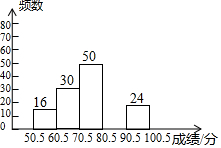 某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
请根据所给信息,解答下列问题:
(1)表中m=80,n=0.12;
(2)补全频数分布直方图;
(3)若成绩超过80分为优秀,分别求出被抽取的学生中优秀的学生频数和频率.
 某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.| 组别 | 分数段 | 频数 | 频率 |
| 一 | 50.5-60.5 | 16 | 0.08 |
| 二 | 60.5-70.5 | 30 | 0.15 |
| 三 | 70.5-80.5 | 50 | 0.25 |
| 四 | 80.5-90.5 | m | 0.40 |
| 五 | 90.5-100.5 | 24 | n |
(1)表中m=80,n=0.12;
(2)补全频数分布直方图;
(3)若成绩超过80分为优秀,分别求出被抽取的学生中优秀的学生频数和频率.
3.已知正比例函数y=(k-2)x的图象经过第一、三象限,则k的值可能是( )
| A. | -2 | B. | 2 | C. | 3 | D. | 0 |

 一次函数y=kx+b(k≠0)的图象经过点(-1,-4)和(2,2)
一次函数y=kx+b(k≠0)的图象经过点(-1,-4)和(2,2)