题目内容
11．先化简，再求值已知$\frac{1}{a}$-1=0，求（$\frac{a-3}{{a}^{2}+3a}$-$\frac{a-1}{{a}^{2}+6a+9}$）÷$\frac{a-9}{a+3}$的值．
分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，求出a的值代入计算即可求出值．
解答 解：原式=[$\frac{a-3}{a（a+3）}$-$\frac{a-1}{（a+3）^{2}}$]•$\frac{a+3}{a-9}$=$\frac{a-9}{a（a+3）^{2}}$•$\frac{a+3}{a-9}$=$\frac{1}{a（a+3）}$，
当$\frac{1}{a}$-1=0，即a=1时，原式=$\frac{1}{4}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
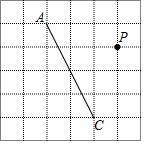如图，在方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．
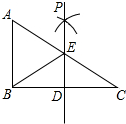如图，已知在Rt△ABC中，∠ABC=90°，点D是BC边的中点，分别以B、C为圆心，大于线段BC长度一半的长为半径画弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接BE，则下列结论：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④ED=$\frac{1}{2}$AB中，一定正确的是①②④．（写序号）
16．某工艺厂计划一周生产工艺品2100个，要求每天生产300个，但实际每天生产量与计划相比有出入，如表是某周的生产情况（超产记为正、减产记为负）：
（1）该厂星期一生产工艺品的数量为316个；
（2）本周产量中最多的一天比最少的一天多生产26个工艺品；
（3）求该工艺厂在本周实际生产工艺品多少个？
（4）已知该厂实际每日计件工资制，每生产一个工艺品可得60元，若超额完成任务，则超过部分每个另奖50元，少生产一个扣80元，求该工艺厂在这一周应付出的工资总额是多少元？
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 增减（单位：个） | +5 | -2 | -5 | +15 | -10 | +16 | -9 |
（2）本周产量中最多的一天比最少的一天多生产26个工艺品；
（3）求该工艺厂在本周实际生产工艺品多少个？
（4）已知该厂实际每日计件工资制，每生产一个工艺品可得60元，若超额完成任务，则超过部分每个另奖50元，少生产一个扣80元，求该工艺厂在这一周应付出的工资总额是多少元？
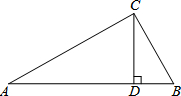如图在△ABC中，CD是AB上的高且CD2=AD•BD，求证：△ABC是直角三角形．
20．下列图形中，既是中心对称图形又是轴对称图形的是（ ）
| A． | 正五边形 | B． | 平行四边形 | C． | 矩形 | D． | 等边三角形 |
高考英语听力测试期间，需要杜绝考点周围的噪音，如图，点A是某市一高考考点，在位于A考点南偏西15°方向距离125米的C处有一消防队，在听力考试期间，消防队突然接到报警电话，告知在位于C点北偏东75°方向的F点处突发火灾，消防队必须立即赶往救火．已知消防车的警报声传播半径为100米，若消防车的警报声对听力测试造成影响，则消防车必须改进行驶，试问：消防车是否需要改道行驶？请说明理由．