题目内容

分解因式：m3n2-m3．
考点：提公因式法与公式法的综合运用
专题：
分析：先提取公因式m3，再对余下的多项式利用平方差公式继续分解．
解答：解：m3n2-m3
=m3（n2-1）
=m3（n+1）（n-1）．
点评：本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．
练习册系列答案
相关题目
如图，OE平分∠AOB，EC⊥OA于点C，ED⊥OB于点D．求证：OE垂直平分CD．
解方程组：
x+y+z=17，①
2x-y-2z=1，②
3x+y-4z=3．③
．
计算：
（1）（x+5y）2-（x-5y）2      
（2）2（x+y）2-2y（y+2x）
二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表：
 x-101 3
 y-13 53 
下列结论：
（1）abc＜0；
（2）当x＞2时，y的值随x的增大而减小；
（3）1是方程ax2+bx+c=5的一个根；
（4）二次函数y=ax2+bx+c开口向上．
其中正确的个数为（　　）
A、4个B、3个C、2个D、1个
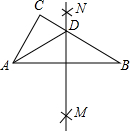如图，在△ABC中，分别以点A和点B为圆心，大于
1
2
AB的长为半径画弧，两弧相交于点M、N．作直线MN，交BC于点D，连结AD．若△ADC的周长为10，AB=7，则△ABC的周长为（　　）
A、20B、17C、14D、7
已知2是关于x的方程x-2a=1的解，则a的值是（　　）
A、-
1
2
B、-
3
2
C、5
D、
1
2
如图，?ABCD的对角线AC，BD交于点O，OE交BC于点E，交AB的延长线于点F，若AB=8，BC=6，BF=5，求BE的长．
在△ABC中，若sinA=
2
2
，tanB=
3
，则∠C=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网