题目内容
二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
下列结论:
(1)abc<0;
(2)当x>2时,y的值随x的增大而减小;
(3)1是方程ax2+bx+c=5的一个根;
(4)二次函数y=ax2+bx+c开口向上.
其中正确的个数为( )
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
(1)abc<0;
(2)当x>2时,y的值随x的增大而减小;
(3)1是方程ax2+bx+c=5的一个根;
(4)二次函数y=ax2+bx+c开口向上.
其中正确的个数为( )
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:二次函数的性质
专题:
分析:利用待定系数法求出二次函数解析式为y=-x2+3x+3,然后判断出①正确,②正确,再根据一元二次方程的解法和二次函数与不等式的关系判定③④即可.
解答:解:∵x=-1时y=-1,x=0时,y=3,x=1时,y=5,
∴
,
解得
∴y=-x2+3x+3,
∴ac=-1×3×3=-9<0,故①正确;
对称轴为直线x=
,
所以,当x>
时,y的值随x值的增大而减小,故②正确;
方程为-x2+2x+3=5,
整理得,x2-2x+2=0,
此方程无解,
所以,1是方程ax2+bx+c=5的一个根错误,故③错误;
a=-1<0开口向下,故④错误;
综上所述,结论正确的是①②.
故选C.
∴
|
解得
|
∴y=-x2+3x+3,
∴ac=-1×3×3=-9<0,故①正确;
对称轴为直线x=
| 3 |
| 2 |
所以,当x>
| 3 |
| 2 |
方程为-x2+2x+3=5,
整理得,x2-2x+2=0,
此方程无解,
所以,1是方程ax2+bx+c=5的一个根错误,故③错误;
a=-1<0开口向下,故④错误;
综上所述,结论正确的是①②.
故选C.
点评:本题考查了二次函数的性质,主要利用了待定系数法求二次函数解析式,二次函数的增减性,二次函数与不等式,根据表中数据求出二次函数解析式是解题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 如图所示,AC、BD相交于点O,且AO=CO,BD=DO.则图中全等三角形有( )对.
如图所示,AC、BD相交于点O,且AO=CO,BD=DO.则图中全等三角形有( )对.| A、4 | B、3 | C、2 | D、1 |
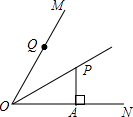 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )| A、4 | B、1 | C、3 | D、2 |
计算(-2)-3的结果为( )
| A、-5 | ||
| B、6 | ||
| C、-8 | ||
D、-
|
下列计算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠ABC=25°,∠BCA=105°,则∠DAE的度数是
如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠ABC=25°,∠BCA=105°,则∠DAE的度数是