题目内容
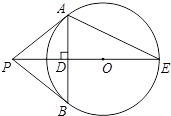 如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE.
如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE.(1)求证:PA是⊙O的切线;
(2)如果OD=3,tan∠AEP=
| 1 |
| 2 |
考点:切线的判定,勾股定理
专题:
分析:(1)连接OA、OB,根据垂径定理的知识,得出OA=OB,∠POA=∠POB,继而证明△PAO≌△PBO,然后利用全等三角形的性质结合切线的判定定理即可得出结论.
(2)根据tan∠AEP=
得出
=
,设AD=x,DE=2x,在Rt△AOD中,由勾股定理得出x,进而就可求得⊙O的半径.
(2)根据tan∠AEP=
| 1 |
| 2 |
| AD |
| DE |
| 1 |
| 2 |
解答: (1)证明:如图,连结OA,OB,
(1)证明:如图,连结OA,OB,
∵PB是⊙O的切线,
∴∠PBO=90°,
∵OA=OB,BA⊥PE于点D,
∴∠POA=∠POB,
在△PAO和△PBO中,
,
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO=90°,
∴PA⊥OA,
∴直线PA为⊙O的切线,
(2)在Rt△ADE中,∠ADE=90°,
∵tan∠AEP=
=
,
∴设AD=x,DE=2x,
∴OE=2x-3.
在Rt△AOD中,由勾股定理,得
(2x-3)2=x2+32,
解得x1=4,x2=0(不合题意,舍去),
∴AD=4,OA=OE=2x-3=5,
即⊙O的半径的长5.
 (1)证明:如图,连结OA,OB,
(1)证明:如图,连结OA,OB,∵PB是⊙O的切线,
∴∠PBO=90°,
∵OA=OB,BA⊥PE于点D,
∴∠POA=∠POB,
在△PAO和△PBO中,
|
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO=90°,
∴PA⊥OA,
∴直线PA为⊙O的切线,
(2)在Rt△ADE中,∠ADE=90°,
∵tan∠AEP=
| AD |
| DE |
| 1 |
| 2 |
∴设AD=x,DE=2x,
∴OE=2x-3.
在Rt△AOD中,由勾股定理,得
(2x-3)2=x2+32,
解得x1=4,x2=0(不合题意,舍去),
∴AD=4,OA=OE=2x-3=5,
即⊙O的半径的长5.
点评:此题考查了切线的判定与性质、勾股定理、全等三角形的判定与性质,综合考查的知识点较多,关键是熟练掌握一些基本性质和定理,在解答综合题目能灵活运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 如图,线段AD到线段BC的运动可能是( )
如图,线段AD到线段BC的运动可能是( )| A、向上平移2格,再向右平移3格 |
| B、向上平移2格,再向左平移1格 |
| C、向上平移1格,再向左平移2格 |
| D、向上平移1格,再向右平移3格 |
 有理数a、b、c在数轴上的位置如图所示,化简式子:|b|+|a-c|+|b-c|-|a-b|的值为:
有理数a、b、c在数轴上的位置如图所示,化简式子:|b|+|a-c|+|b-c|-|a-b|的值为: 如图,∠AOD=70°,OB是∠AOC的平分线,∠AOB=20°,求∠AOC、∠COD.
如图,∠AOD=70°,OB是∠AOC的平分线,∠AOB=20°,求∠AOC、∠COD. 如图,是一个底面半径为1cm,高度为2πcm的无盖圆柱形玻璃容器,A、B两点在容器顶部一条直径的两端,现有一只小甲虫在容器外A点正下方1cm的M处,要爬到容器内B点正下方距离底部1cm的N处,则这只小甲虫最短爬行的距离是
如图,是一个底面半径为1cm,高度为2πcm的无盖圆柱形玻璃容器,A、B两点在容器顶部一条直径的两端,现有一只小甲虫在容器外A点正下方1cm的M处,要爬到容器内B点正下方距离底部1cm的N处,则这只小甲虫最短爬行的距离是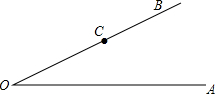 如图:点C是∠AOB的边OB上的一点,按下列要求画图并回答问题.
如图:点C是∠AOB的边OB上的一点,按下列要求画图并回答问题.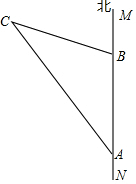 如图,直线MN是沿海边南北方向的一条公路,某施工队在公路的A点测得北偏西30°的方向上有一栋别墅C,沿正北方向走了400米到达B点后,测得别墅C在北偏西75°的方向上,现要从别墅C修一条通向公路MN的最短的小路,请你求出这条小路的长.
如图,直线MN是沿海边南北方向的一条公路,某施工队在公路的A点测得北偏西30°的方向上有一栋别墅C,沿正北方向走了400米到达B点后,测得别墅C在北偏西75°的方向上,现要从别墅C修一条通向公路MN的最短的小路,请你求出这条小路的长.