题目内容
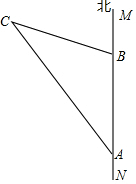 如图,直线MN是沿海边南北方向的一条公路,某施工队在公路的A点测得北偏西30°的方向上有一栋别墅C,沿正北方向走了400米到达B点后,测得别墅C在北偏西75°的方向上,现要从别墅C修一条通向公路MN的最短的小路,请你求出这条小路的长.
如图,直线MN是沿海边南北方向的一条公路,某施工队在公路的A点测得北偏西30°的方向上有一栋别墅C,沿正北方向走了400米到达B点后,测得别墅C在北偏西75°的方向上,现要从别墅C修一条通向公路MN的最短的小路,请你求出这条小路的长.考点:解直角三角形的应用-方向角问题
专题:
分析:首先作BD⊥AC于点D,作CE⊥AB于点E,进而得出△CDB为等腰直角三角形,再利用CE=
AC求出即可.
| 1 |
| 2 |
解答: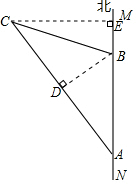 解:作BD⊥AC于点D,作CE⊥AB于点E,
解:作BD⊥AC于点D,作CE⊥AB于点E,
∵AB=400米,
∴BD=400sin30°=200,AD=400cos30°=200
(米),
∵△CDB为等腰直角三角形,
CD=BD=200(米),
Rt△ACE中,∠CAE=30° AC=200+200
(米),
∴CE=
AC=100+100
(米),
答:这条小路的长为(100+100
)米.
 解:作BD⊥AC于点D,作CE⊥AB于点E,
解:作BD⊥AC于点D,作CE⊥AB于点E,∵AB=400米,
∴BD=400sin30°=200,AD=400cos30°=200
| 3 |
∵△CDB为等腰直角三角形,
CD=BD=200(米),
Rt△ACE中,∠CAE=30° AC=200+200
| 3 |
∴CE=
| 1 |
| 2 |
| 3 |
答:这条小路的长为(100+100
| 3 |
点评:此题主要考查了方向角问题的应用,根据已知得出△CDB为等腰直角三角形以及在直角三角形中求出AC的长是解题关键.

练习册系列答案
相关题目
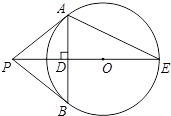 如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE.
如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE.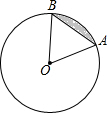 如图,⊙O的半径为2,AB是⊙O的一条弦,∠O=60°,则图中阴影弓形的面积为
如图,⊙O的半径为2,AB是⊙O的一条弦,∠O=60°,则图中阴影弓形的面积为 在正方形网格中,△ABC的位置如图所示,则tanB的值为
在正方形网格中,△ABC的位置如图所示,则tanB的值为 已知二次函数y=x2+bx+c的图象经过点(-4,3)、(-3,0).
已知二次函数y=x2+bx+c的图象经过点(-4,3)、(-3,0).