题目内容
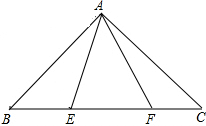 已知如图,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2.
已知如图,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2.考点:勾股定理,等腰三角形的性质
专题:证明题
分析:首先把△ACF绕点A顺时针旋转90°,得到△ABG.连接EG,可得△ACF≌△ABG.进而得到AG=AF,BG=CF,∠ABG=∠ACF=45°,然后再证明△AEG≌△AFE可得EF=EG,再利用勾股定理可得结论.
解答: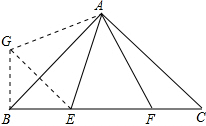 证明:把△ACF绕点A顺时针旋转90°,得到△ABG.连接EG.
证明:把△ACF绕点A顺时针旋转90°,得到△ABG.连接EG.
则△ACF≌△ABG.
∴AG=AF,BG=CF,∠ABG=∠ACF=45°.
∵∠BAC=90°,∠GAF=90°.
∴∠GAE=∠EAF=45°,
在△AEG和△AFE中
,
∴△AEG≌△AFE(SAS).
∴EF=EG,
又∠GBE=90°,
∴BE2+BG2=EG2,
即BE2+CF2=EF2.
 证明:把△ACF绕点A顺时针旋转90°,得到△ABG.连接EG.
证明:把△ACF绕点A顺时针旋转90°,得到△ABG.连接EG.则△ACF≌△ABG.
∴AG=AF,BG=CF,∠ABG=∠ACF=45°.
∵∠BAC=90°,∠GAF=90°.
∴∠GAE=∠EAF=45°,
在△AEG和△AFE中
|
∴△AEG≌△AFE(SAS).
∴EF=EG,
又∠GBE=90°,
∴BE2+BG2=EG2,
即BE2+CF2=EF2.
点评:此题主要考查了等腰三角形的性质,旋转的性质,关键是证明作出辅助线,证明△AEG≌△AFE.

练习册系列答案
相关题目
抛物线y=(x+3)2-4的对称轴为( )
| A、直线x=3 |
| B、直线x=-3 |
| C、直线x=4 |
| D、直线x=-4 |
 如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则CF:AB的值为( )
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则CF:AB的值为( )| A、1:3 | B、2:3 |
| C、3:4 | D、1:2 |
 如图,P是边长为1的正六边形对角线CD上一点,则AP+BP的最小值为( )
如图,P是边长为1的正六边形对角线CD上一点,则AP+BP的最小值为( )| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
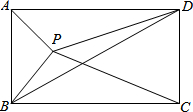 如图,在平行四边形ABCD中,P是△BAD内一点.若△PAB的面积为2,△PCB的面积为5,求△PBD的面积.
如图,在平行四边形ABCD中,P是△BAD内一点.若△PAB的面积为2,△PCB的面积为5,求△PBD的面积. 如图是由若干小立方块搭成的几何体的俯视图,正方形内的数字表示在该位置上小立方块的块数,根据左视图所提供的信息,试确定x、y的值.
如图是由若干小立方块搭成的几何体的俯视图,正方形内的数字表示在该位置上小立方块的块数,根据左视图所提供的信息,试确定x、y的值. 如图,A、B两个乡镇相距21千米,原计划在两乡镇之间修一条笔直公路以改善交通状况,现在情况有变,为保护环境,县政府决定在以C处为中心方圆10千米的圆形区域内建立绿色生态旅游区,不允许公路从生态区穿过,C处距离A、B两个乡镇分别为20千米和13千米,请通过计算回答,两乡镇间的公路还能按计划实施吗?
如图,A、B两个乡镇相距21千米,原计划在两乡镇之间修一条笔直公路以改善交通状况,现在情况有变,为保护环境,县政府决定在以C处为中心方圆10千米的圆形区域内建立绿色生态旅游区,不允许公路从生态区穿过,C处距离A、B两个乡镇分别为20千米和13千米,请通过计算回答,两乡镇间的公路还能按计划实施吗?