题目内容
 如图,P是边长为1的正六边形对角线CD上一点,则AP+BP的最小值为( )
如图,P是边长为1的正六边形对角线CD上一点,则AP+BP的最小值为( )| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
考点:轴对称-最短路线问题,正多边形和圆
专题:
分析:连接BE、AE,则AE的长即为AP+PB的最小值,再根据锐角三角函数的定义求出BF的长,根据勾股定理即可得出AE的长,进而得出结论.
解答: 解:连接BE、AE,
解:连接BE、AE,
∵多边形是正六边形,
∴AE的长即为AP+PB的最小值,
∴∠BDC=60°,
∴BF=BD•sin60°=
,
同理EF=
,
∴BE=
,
∴AE=
=
=2,即AP+BP的最小值为2.
故选C.
 解:连接BE、AE,
解:连接BE、AE,∵多边形是正六边形,
∴AE的长即为AP+PB的最小值,
∴∠BDC=60°,
∴BF=BD•sin60°=
| ||
| 2 |
同理EF=
| ||
| 2 |
∴BE=
| 3 |
∴AE=
| AB2+BE2 |
12+(
|
故选C.
点评:本题考查的是轴对称-最短路线问题,熟知轴对称的性质及正六边形的性质是解答此题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
下列各题计算正确的是( )
| A、(a-3b)(-6a)=-6a2-18ab | ||
B、(-
| ||
C、(-
| ||
| D、-3x(2x2-x+1)=-6x3+3x2-3x |
关于x的方程(k+2)x|k|-4=0是一元二次方程,则k的值是( )
| A、±2 | B、-2 | C、2 | D、-3 |
某工人原计划每天生产a个零件,现实际每天多生产b个零件,则生产m个零件提前的天数为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列数据能作为三角形三边长的一组是( )
| A、1cm、2cm、3cm |
| B、1cm、2cm、4cm |
| C、2cm、3cm、4cm |
| D、4cm、4cm、9cm |
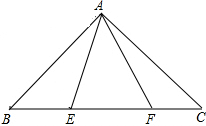 已知如图,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2.
已知如图,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2.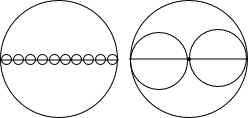 如图,两个大小相同的大圆,其中一个大圆内有10个小圆,另一个大圆内有2个小圆,你认为大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大?请你猜一猜,并用学过的知识和数学方法验证你的猜想.
如图,两个大小相同的大圆,其中一个大圆内有10个小圆,另一个大圆内有2个小圆,你认为大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大?请你猜一猜,并用学过的知识和数学方法验证你的猜想.