题目内容
抛物线y=（x+3）2-4的对称轴为（ ）
| A、直线x=3 |
| B、直线x=-3 |
| C、直线x=4 |
| D、直线x=-4 |
考点：二次函数的性质
专题：
分析：直接根据抛物线顶点式的特殊形式可知对称轴．
解答：解：因为抛物线y=-（x+3）2-4是顶点式，
顶点坐标是（-3，-4），
故对称轴是直线x=-3．
故选：B．
顶点坐标是（-3，-4），
故对称轴是直线x=-3．
故选：B．
点评：此题主要考查了求抛物线的对称轴的方法，比较简单．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
如图，矩形ABCD中，AB=6cm，BC=3cm，E是DC的中点，BF=
如图，AB∥CD，DB⊥BC，∠2=55°，则∠1的度数是（ ）| A、35° | B、45° |
| C、55° | D、145° |
抛物线y=x2+6x+10的顶点坐标是（ ）
| A、（3，1） |
| B、（-3，1） |
| C、（-9，1） |
| D、（9，-1） |
平面内第四象限有一点，它到x轴的距离为4，它到y轴的距离为3，则它的坐标为（ ）
| A、（4，-3） |
| B、（-4，3） |
| C、（-3，4） |
| D、（3，-4） |
下列各题计算正确的是（ ）
| A、（a-3b）（-6a）=-6a2-18ab | ||
B、(-
| ||
C、(-
| ||
| D、-3x（2x2-x+1）=-6x3+3x2-3x |
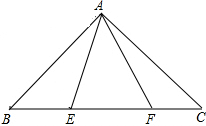已知如图，△ABC中，∠CAB=90°，AB=AC，E、F为BC上的点且∠EAF=45°，求证：EF2=BE2+FC2．