题目内容
1.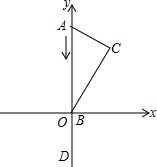 如图,将含30°的直角三角尺放在如图所示的直角坐标系中,点A(0,4),点B在原点,∠C=90°,∠ABC=30°,D点与A点关于原点对称,A点向D点运动,到达D点后停止.B点在x轴上运动.当A到达D时,点C走过的路径长为4$\sqrt{3}$.
如图,将含30°的直角三角尺放在如图所示的直角坐标系中,点A(0,4),点B在原点,∠C=90°,∠ABC=30°,D点与A点关于原点对称,A点向D点运动,到达D点后停止.B点在x轴上运动.当A到达D时,点C走过的路径长为4$\sqrt{3}$.
分析 画图可知,点C运动的轨迹是一条线段,由此画出图形解答即可.
解答 解:如图: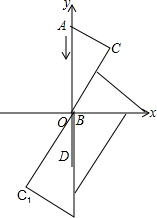
点C运动的轨迹是线段CC1,
∵A(0,4),∠C=90°,∠ABC=30°,
∴AB=4,
∴BC=AB•cos∠B=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴CC1=2BC=4$\sqrt{3}$,
∴点C走过的路径长为4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 此题考查点的运动轨迹,特殊角的三角函数,画出图形,得出运动轨迹经过的路径是解决问题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
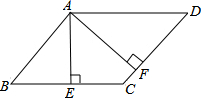 如图,?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=135°.
如图,?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=135°.
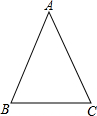 如图,△ABC中,AB=AC=20,cosC=$\frac{\sqrt{5}}{5}$.
如图,△ABC中,AB=AC=20,cosC=$\frac{\sqrt{5}}{5}$.