题目内容
8.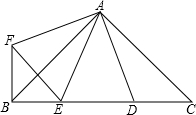 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )| A. | △AED≌△AEF | B. | △ABE∽△ACD | C. | BE+DC>DE | D. | BE2+DC2=DE2 |
分析 A、根据∠DAF=90°,∠DAE=45°,得出∠FAE=45°,利用SAS证明△AED≌△AEF,判定A正确;
B、如果△ABE∽△ACD,那么∠BAE=∠CAD,由∠ABE=∠C=45°,则∠AED=∠ADE,AD=AE,而由已知不能得出此条件,判定B错误;
C、先由∠BAC=∠DAF=90°,得出∠CAD=∠BAF,再利用SAS证明△ACD≌△ABF,得出CD=BF,又①知DE=EF,那么在△BEF中根据三角形两边之和大于第三边可得BE+BF>EF,等量代换后判定C正确;
D、先由△ACD≌△ABF,得出∠C=∠ABF=45°,进而得出∠EBF=90°,然后在Rt△BEF中,运用勾股定理得出BE2+BF2=EF2,等量代换后判定D正确.
解答 解:A、∵∠DAF=90°,∠DAE=45°,
∴∠FAE=∠DAF-∠DAE=45°.
在△AED与△AEF中,
$\left\{\begin{array}{l}{AD=AF}\\{∠DAE=∠FAE=45°}\\{AE=AE}\end{array}\right.$,
∴△AED≌△AEF(SAS).
故本选项错误;
B、∵∠BAC=90°,AB=AC,
∴∠ABE=∠C=45°.
∵点D、E为BC边上的两点,∠DAE=45°,
∴AD与AE不一定相等,∠AED与∠ADE不一定相等,
∵∠AED=45°+∠BAE,∠ADE=45°+∠CAD,
∴∠BAE与∠CAD不一定相等,
∴△ABE与△ACD不一定相似.
故本选项正确;
C、∵∠BAC=∠DAF=90°,
∴∠BAC-∠BAD=∠DAF-∠BAD,即∠CAD=∠BAF.
在△ACD与△ABF中,
$\left\{\begin{array}{l}{AC=AB}\\{∠CAD=∠BAF}\\{AD=AF}\end{array}\right.$,
∴△ACD≌△ABF(SAS),
∴CD=BF,
由A选项知,△AED≌△AEF,
∴DE=EF.
在△BEF中,∵BE+BF>EF,
∴BE+DC>DE.
故本选项错误;
D、由C选项知,△ACD≌△ABF,
∴∠C=∠ABF=45°,
∵∠ABE=45°,
∴∠EBF=∠ABE+∠ABF=90°.
在Rt△BEF中,由勾股定理,得BE2+BF2=EF2,
∵BF=DC,EF=DE,
∴BE2+DC2=DE2.
故本选项错误.
故选:B.
点评 本题考查了勾股定理,全等三角形的判定与性质,等腰直角直角三角形的性质,三角形三边关系定理,相似三角形的判定,此题涉及的知识面比较广,解题时要注意仔细分析,有一定难度.

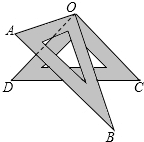 如图,将一幅三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是( )
如图,将一幅三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是( )| A. | ∠BOD | B. | ∠ABO | C. | ∠BOC | D. | ∠BAO |
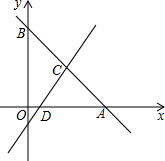 如图,在平面直角坐标系中,直线y=-x+8分别交两轴于点A、B,点C为线段AB的中点,点D在线段OA上,且CD的长是方程$\frac{2}{x+1}=\frac{1}{x-2}$的根.
如图,在平面直角坐标系中,直线y=-x+8分别交两轴于点A、B,点C为线段AB的中点,点D在线段OA上,且CD的长是方程$\frac{2}{x+1}=\frac{1}{x-2}$的根.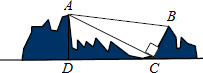 如图,某景区有一出索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,求山峰顶点A到C点的水平面高度AD.(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)
如图,某景区有一出索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,求山峰顶点A到C点的水平面高度AD.(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)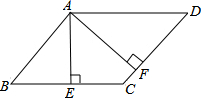 如图,?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=135°.
如图,?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=135°.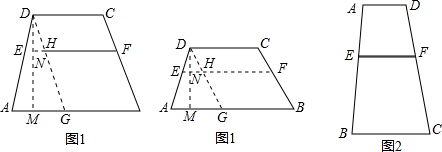 如图1,四边形ABCD中,AB∥CD,AB=a,CD=b(a≠b),点E、F分别是AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2.
如图1,四边形ABCD中,AB∥CD,AB=a,CD=b(a≠b),点E、F分别是AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2.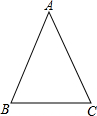 如图,△ABC中,AB=AC=20,cosC=$\frac{\sqrt{5}}{5}$.
如图,△ABC中,AB=AC=20,cosC=$\frac{\sqrt{5}}{5}$.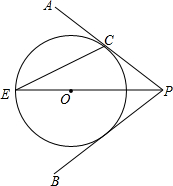 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C. 已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=$\frac{k}{x}$(x>0)经过点D,交BC的延长线于点E,且OB•AC=160,有下列四个结论:
已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=$\frac{k}{x}$(x>0)经过点D,交BC的延长线于点E,且OB•AC=160,有下列四个结论: