题目内容
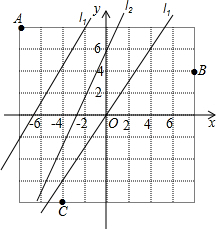 某地区(如图)计划在A,B两城市之间和A,C两城市之间各建一条高速公路.高速公路与其他道路(图中用直线l1,l2,l3表示)交叉处需建立交桥,用坐标表示各立交桥的位置.
某地区(如图)计划在A,B两城市之间和A,C两城市之间各建一条高速公路.高速公路与其他道路(图中用直线l1,l2,l3表示)交叉处需建立交桥,用坐标表示各立交桥的位置.考点:作图—应用与设计作图
专题:
分析:求出各直线的解析式,组成方程组求解即可.
解答: 解:设AB解析式为y=kx+b,
解:设AB解析式为y=kx+b,
把(-8,8),(8,4)分别代入解析式得
,解得
,
故AB解析式为y=-
x+6;
设AC解析式为y=kx+b,
把(-8,8),(-4,-8)分别代入解析式得
,解得
,
故AC解析式为y=-4x-24.
设l1解析式为y=kx+b,
把(-2,8),(-8,-2)分别代入解析式得
,解得
,
故l1解析式为y=
x+
,
设l2解析式为y=kx+b,
把(0,6),(-2,2)分别代入解析式得
,解得
,
故l2解析式为y=2x+6;
设l3解析式为y=kx,
把(4,6)代入解析式得4k=6,解得k=
,
设l3解析式为y=
x.
AB和 l1组成方程组得
,解得
;
AB和 l2组成方程组得
,解得
;
AB和 l3组成方程组得
,解
;
AC和 l1组成方程组得
,解得
;
AC和 l2组成方程组得
,解得
;
AC和 l3组成方程组得
,解得
.
可知,各立交桥的坐标为(-
,
)(0,6)(
,
)(-
,
)(-5,-4)(-
,-
).
 解:设AB解析式为y=kx+b,
解:设AB解析式为y=kx+b,把(-8,8),(8,4)分别代入解析式得
|
|
故AB解析式为y=-
| 1 |
| 4 |
设AC解析式为y=kx+b,
把(-8,8),(-4,-8)分别代入解析式得
|
|
故AC解析式为y=-4x-24.
设l1解析式为y=kx+b,
把(-2,8),(-8,-2)分别代入解析式得
|
|
故l1解析式为y=
| 5 |
| 3 |
| 34 |
| 3 |
设l2解析式为y=kx+b,
把(0,6),(-2,2)分别代入解析式得
|
|
故l2解析式为y=2x+6;
设l3解析式为y=kx,
把(4,6)代入解析式得4k=6,解得k=
| 3 |
| 2 |
设l3解析式为y=
| 3 |
| 2 |
AB和 l1组成方程组得
|
|
AB和 l2组成方程组得
|
|
AB和 l3组成方程组得
|
|
AC和 l1组成方程组得
|
|
AC和 l2组成方程组得
|
|
AC和 l3组成方程组得
|
|
可知,各立交桥的坐标为(-
| 64 |
| 23 |
| 154 |
| 23 |
| 24 |
| 7 |
| 36 |
| 7 |
| 106 |
| 17 |
| 24 |
| 17 |
| 48 |
| 11 |
| 72 |
| 11 |
点评:本题考查了作图--应用与设计作图,与一次函数相结合组成方程组是解题的关键.

练习册系列答案
相关题目
下列命题中,正确的命题是( )
| A、圆的切线垂直于圆的半径 |
| B、经过三个点一定可以作圆 |
| C、三角形的外心到三角形各顶点的距离都相等 |
| D、平分弦的直径必垂直于弦 |
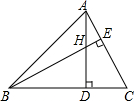 如图,在△ABC中,∠ABC=45°,AC=8,H是高AD和BE的交点,则线段BH的长度为
如图,在△ABC中,∠ABC=45°,AC=8,H是高AD和BE的交点,则线段BH的长度为 如图,将一张三角形纸片ABC(如图)折叠,点A落在A′处,若要使折痕DE∥BC,则应怎么折?
如图,将一张三角形纸片ABC(如图)折叠,点A落在A′处,若要使折痕DE∥BC,则应怎么折? 如图,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐,请问壁虎从A处到B处的最短路线是什么?
如图,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐,请问壁虎从A处到B处的最短路线是什么?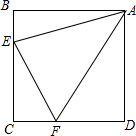 如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小.
如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小. 如图,在梯形ABCD中,已知AE平分∠BAD,AB=AD+BC,E是CD的中点.求证:BE平分∠ABC.
如图,在梯形ABCD中,已知AE平分∠BAD,AB=AD+BC,E是CD的中点.求证:BE平分∠ABC.