题目内容
10.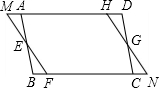 如图四边形ABCD、MFNH都是平行四边形,MAHD和BFCN都在一直线上,HD=FB.
如图四边形ABCD、MFNH都是平行四边形,MAHD和BFCN都在一直线上,HD=FB.求证:(1)MA=CN;(2)∠AEM=∠CGN.
分析 (1)由四边形ABCD、MFNH都是平行四边形,推出MH=FN,AD=BC,由DH=BF,推出AD-DH=BC-FC,即AH=CF,推出MH-AH=FN-FC,即AM=CN,
(2)由四边形ABCD、MFNH都是平行四边形,推出∠EAH=∠BCG,∠M=∠N,由∠EAH=∠M+∠AEM,∠BCG=∠N+∠CGN,推出∠M+∠AEM=∠N+∠CGN,即可证明∠AEM=∠CGN.
解答 证明:(1)∵四边形ABCD、MFNH都是平行四边形,
∴MH=FN,AD=BC,
∵DH=BF,
∴AD-DH=BC-FC,即AH=CF,
∴MH-AH=FN-FC,即AM=CN,
∴AM=CN.
(2))∵四边形ABCD、MFNH都是平行四边形,
∴∠EAH=∠BCG,∠M=∠N,
∵∠EAH=∠M+∠AEM,∠BCG=∠N+∠CGN,
∴∠M+∠AEM=∠N+∠CGN,
∴∠AEM=∠CGN.
点评 本题考查平行四边形的性质、三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题,属于基础题,中考常考题型.

练习册系列答案
相关题目
20.下列属于一元一次方程的是( )
| A. | x+1 | B. | 3x+2x=2 | C. | 5x-5=4y-4 | D. | x2-2x+1=0 |
18.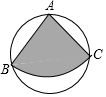 如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为( )
如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为( )
 如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为( )
如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为( )| A. | 4-$\frac{π}{9}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
15.二次函数y=(x-1)2-2图象的对称轴是( )
| A. | 直线x=1 | B. | 直线x=-1 | C. | 直线x=2 | D. | 直线x=-2 |
19.下列说法中,正确的是( )
| A. | 为检测市场上正在销售的酸奶质量,应该采用全面调查的方式 | |
| B. | 在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 | |
| C. | 小强班上有3个同学都是16岁,因此小强认为他们班学生年龄的众数是16岁 | |
| D. | 给定一组数据,则这组数据的中位数一定只有一个 |
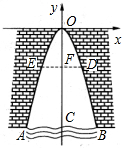 某涵洞的截面边缘成抛物线形,现测得当水面宽AB=2米时涵洞的顶点与水面的距离为4米,这时离开水面2米处涵洞宽DE是多少?
某涵洞的截面边缘成抛物线形,现测得当水面宽AB=2米时涵洞的顶点与水面的距离为4米,这时离开水面2米处涵洞宽DE是多少?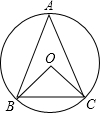 如图所示,△ABC内接于⊙O,AB=AC,∠BOC=120°.求$\widehat{AB}$和$\widehat{AC}$的度数.
如图所示,△ABC内接于⊙O,AB=AC,∠BOC=120°.求$\widehat{AB}$和$\widehat{AC}$的度数.
