题目内容
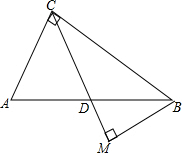 在Rt△ABC中,∠ACB=90°,D是边AB的中点,BM⊥CD于点M,已知AC=6,tanA=
在Rt△ABC中,∠ACB=90°,D是边AB的中点,BM⊥CD于点M,已知AC=6,tanA=| 4 |
| 3 |
(1)求线段CD的长;
(2)求sin∠BDM的值.
考点:相似三角形的判定与性质,勾股定理
专题:常规题型
分析:(1)在Rt△ABC中,根据tanA=
和AC=6即可求得CD的长;
(2)可证△CMB∽△BCA,即可求得BM的长,即可解题.
| 4 |
| 3 |
(2)可证△CMB∽△BCA,即可求得BM的长,即可解题.
解答:解 (1)在Rt△ABC中,∠ACB=90°,
tanA=
=
,
∴BC=
×6=8,
∴AB=
=
=10,
∵D是边AB的中点,
∴CD=DB=
AB=
×10=5.
(2)∵CD=DB,
∴∠DCB=∠DBC,
又∵BM⊥CD于点M,
∴∠BMC=∠ACB=90°,
∴△CMB∽△BCA,
∴
=
,
∴
=
,
∴BM=
,
∴sin∠BDM=
=
.
tanA=
| BC |
| AC |
| 4 |
| 3 |
∴BC=
| 4 |
| 3 |
∴AB=
| AC2+BC2 |
| 62+82 |
∵D是边AB的中点,
∴CD=DB=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵CD=DB,
∴∠DCB=∠DBC,
又∵BM⊥CD于点M,
∴∠BMC=∠ACB=90°,
∴△CMB∽△BCA,
∴
| BM |
| AC |
| BC |
| AB |
∴
| BM |
| 6 |
| 8 |
| 10 |
∴BM=
| 24 |
| 5 |
∴sin∠BDM=
| BM |
| BD |
| 24 |
| 25 |
点评:本题考查了相似三角形的判定,考查了三角函数的计算.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图是将长方形纸片沿对角线折叠得到的,图中(包括实线、虚线在内) 共有全等三角形( )对.
如图是将长方形纸片沿对角线折叠得到的,图中(包括实线、虚线在内) 共有全等三角形( )对.| A、2 | B、3 | C、4 | D、5 |
 如图,△DEF是正三角形,AD=BF=EC,求证:△ABC是正三角形.
如图,△DEF是正三角形,AD=BF=EC,求证:△ABC是正三角形. 如图,在△ABC中,D是BC上的一点,E是AC上的一点,EF∥AD交BC于F,EG∥AB交BC于G,求证:CF•GB=CG•FD.
如图,在△ABC中,D是BC上的一点,E是AC上的一点,EF∥AD交BC于F,EG∥AB交BC于G,求证:CF•GB=CG•FD.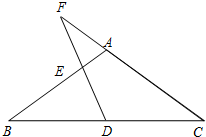 如图,已知在△ABC中,AB=AC=10,BC=16,D是边BC的中点,E是射线BA上一动点,直线DE交射线CA于F点.
如图,已知在△ABC中,AB=AC=10,BC=16,D是边BC的中点,E是射线BA上一动点,直线DE交射线CA于F点. 如图,抛物线y=x2-2x-3与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,点D是该抛物线的顶点,连接AD,BD.
如图,抛物线y=x2-2x-3与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,点D是该抛物线的顶点,连接AD,BD.