题目内容
16．抛物线y=2x2-4x+3绕坐标原点旋转180°所得的抛物线的解析式是y=-2x2-4x-3．分析 根据旋转的性质，可得a的绝对值不变，根据中心对称，可得答案．
解答 解：将y=2x2-4x+3化为顶点式，得y=2（x-1）2+1，
抛物线y=2x2-4x+3绕坐标原点旋转180°所得的抛物线的解析式是y=-2（x+1）2-1，
化为一般式，得
y=-2x2-4x-3，
故答案为：y=-2x2-4x-3．
点评 本题考查了二次函数图象与几何变换，利用了中心对称的性质．
练习册系列答案
相关题目
6．某种超级计算机完成一次基本运算的时间约为0.00000000000011秒，用科学记数法表示这个数为（ ）
| A． | 1.1×10-12 | B． | 1.1×10-13 | C． | 11×10-12 | D． | 11×10-13 |
7．下列说法正确的有几个（ ）
（1）任何一个有理数的平方都是正数
（2）一个数的绝对值越大，表示它的点在数轴上越靠右
（3）0既不是正数也不是负数
（4）符号相反的两个数互为相反数．
（1）任何一个有理数的平方都是正数
（2）一个数的绝对值越大，表示它的点在数轴上越靠右
（3）0既不是正数也不是负数
（4）符号相反的两个数互为相反数．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
11．已知点P（a，b）是反比例函数y=$\frac{1}{x}$图象上异于点（-1，-1）的一个动点，则$\frac{1}{1+a}$+$\frac{1}{1+b}$=（ ）
| A． | 2 | B． | 1 | C． | $\frac{3}{2}$ | D． | $\frac{1}{2}$ |
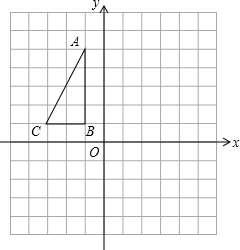如图，在平面直角坐标系中，ABC的顶点的坐标分别为A（-1，5）、B（-1，1）、C（-3，1）．将△ABC向右平移2个单位、再向下平移4个单位得到△A1B1C1；将△ABC绕原点O旋转180°得到△A2B2C2