题目内容
17.如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1,l2,l3之间的距离为2,点A、C分别在直线l2,l1上,(1)利用直尺和圆规作出以AC为底的等腰△ABC,使得点B落在直线l3上(保留作图痕迹,不写作法);
(2)若(1)中得到的△ABC为等腰直角三角形,求AC的长.
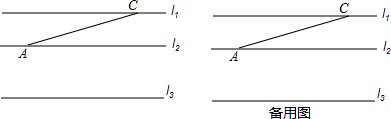
分析 (1)作出线段AC的垂直平分线,使得点B落在直线l3上,连结AB,BC,△ABC即为所求;
(2)过点C作CD⊥l3于D,过点A作AE⊥l3于E,根据同角的余角相等求出∠ABE=∠BCD,然后利用“角角边”证明△ABE和△BCD全等,根据全等三角形对应边相等可得AE=BD,再利用勾股定理列式求出BC的长,然后根据等腰直角三角形的斜边等于直角边的$\sqrt{2}$倍解答.
解答 解:(1)如图1所示:△ABC即为所求.
(2)如图2,过点C作CD⊥l3于D,过点A作AE⊥l3于E,
则∠BCD+∠CBD=90°,
∵△ABC为等腰直角三角形,
∴∠ABE+∠CBD=180°-90°=90°,
∴∠ABE=∠BCD,
在△ABE和△BCD中,
$\left\{\begin{array}{l}{∠AEB=∠BDC}\\{∠ABE=∠BCD}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCD(AAS),
∴AE=BD,
∵l1,l2之间的距离为1,l2,l3之间的距离为2,
∴BD=2,CD=1+2=3,
在Rt△BCD中,BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∵△ABC是等腰直角三角形,
∴AC=$\sqrt{2}$BC=$\sqrt{26}$.
点评 本题考查了全等三角形的判定与性质,线段垂直平分线的画法,平行线间的距离,等腰三角形的性质,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图,数轴上的点A和点B分别表示数a与数b,下列结论中正确的是( )
如图,数轴上的点A和点B分别表示数a与数b,下列结论中正确的是( )
 如图,数轴上的点A和点B分别表示数a与数b,下列结论中正确的是( )
如图,数轴上的点A和点B分别表示数a与数b,下列结论中正确的是( )| A. | a>b | B. | |a|<|b| | C. | a<-b | D. | a+b<0 |
7. “六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.
“六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.
①如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次;
②假如你去转动转盘一次,获得铅笔的概率大约是0.70;
③当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
④转动转盘10次,一定有3次获得文具盒
 “六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.
“六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.①如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次;
②假如你去转动转盘一次,获得铅笔的概率大约是0.70;
③当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
④转动转盘10次,一定有3次获得文具盒
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
| 落在“铅笔”区域的频率$\frac{m}{n}$ | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
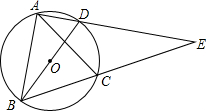 如图,BD是⊙O的直径,A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
如图,BD是⊙O的直径,A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFC=115°,则∠AED′的度数为50度.
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFC=115°,则∠AED′的度数为50度. 如图,已知AD、BC相交于点O,AO=CO,BO=DO.求证:∠A=∠C.
如图,已知AD、BC相交于点O,AO=CO,BO=DO.求证:∠A=∠C.