题目内容
5．先分解因式化简，再求值：（$\frac{x+y}{3}$）2-（$\frac{x-y}{3}$）2，其中x=-$\frac{9}{4}$，y=2010．分析 首先利用完全平方公式化简进而合并同类项，再把已知代入求出答案．
解答 解：∵（$\frac{x+y}{3}$）2-（$\frac{x-y}{3}$）2
=$\frac{{x}^{2}+2xy+{y}^{2}}{9}$-$\frac{{x}^{2}-2xy+{y}^{2}}{9}$
=$\frac{4xy}{9}$，
将x=-$\frac{9}{4}$，y=2010代入上式得：
原式=$\frac{4×（-\frac{9}{4}）×2010}{9}$=-2010．
点评 此题主要考查了完全平方公式的应用，熟练应用完全平方公式是解题关键．
练习册系列答案
中考解读考点精练系列答案
相关题目
15．下列说法：①0是绝对值最小的有理数；②两个数的和一定大于这两个数中的任何一个；③一个数的绝对值等于它的相反数，则这个数是负数；④两个数比较大小，绝对值大的反而小．正确的共有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
求出下列图中x的值．
20．a为任意实数时，下列分式一定有意义的是（ ）
| A． | $\frac{{{a^2}+a}}{a}$ | B． | $\frac{a}{{{a^2}+1}}$ | C． | $\frac{a}{{{a^2}-1}}$ | D． | $\frac{1}{{{a^2}-1}}$ |
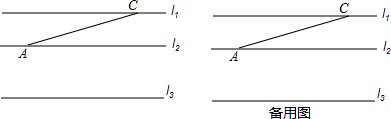
已知△ABC是等边三角形，点D、E分别在AC、BC边上，且AD=CE，AE与BD交于点F，则∠AFD的度数为60°．