题目内容
1.请从A,B两个题目中任选一题作答.A 关于x的方程x2+mx-1=0的一个根是x=2,求m的值.
B 关于x的方程(x+a)2=b的根是x1=-1,x2=2,求方程(x+a+2)2=b的根.
我选择A题.
分析 A、把x=-1代入已知方程列出关于m的新方程,通过解新方程可以求得m的值.
B、把后面一个方程中的x+2看作整体,相当于前面一个方程中的x求解.
解答 解:我选择A题,
A、依题意,得
22+2m-1=0,
解得m=-1.5.
故m的值为-1.5.
我选择B题,
B、∵关于x的方程(x+a)2=b的根是x1=-1,x2=2,
∴方程(x+a+2)2=b变形为[(x+2)+a]2=b,即此方程中x+2=-1或x+2=2,
解得x=-3或x=0.
点评 本题考查的是一元二次方程的解.一元二次方程的解就是能够使方程左右两边相等的未知数的值.即用这个数代替未知数所得式子仍然成立.(2)中注意由两个方程的特点进行简便计算.

练习册系列答案
相关题目
11.方程x2=4的解是( )
| A. | x1=4,x2=-4 | B. | x1=x2=2 | C. | x1=2,x2=-2 | D. | x1=1,x2=4 |
16.一个自然数的算术平方根是a,那么与这个自然数相邻的下一个自然数的平方根是( )
| A. | a+1 | B. | ±$\sqrt{a+1}$ | C. | a2+1 | D. | ±$\sqrt{{a}^{2}+1}$ |
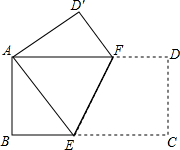 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,
如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,