题目内容
16. 如图,直线y=$\frac{1}{2}$x-2与x轴、y轴分别交于点A和点B,点C在直线AB上,且点C的纵坐标为-1,点D在反比例函数:y=$\frac{k}{x}$的图象上,CD平行于y轴,S△OCD=$\frac{5}{2}$.
如图,直线y=$\frac{1}{2}$x-2与x轴、y轴分别交于点A和点B,点C在直线AB上,且点C的纵坐标为-1,点D在反比例函数:y=$\frac{k}{x}$的图象上,CD平行于y轴,S△OCD=$\frac{5}{2}$.(1)求点A、B、C的坐标;
(2)求点D的坐标;
(3)求k的值.
分析 (1)分别令x=0,y=0,y=-1代入y=$\frac{1}{2}$x-2求出相应x、y的值即可求出点A、B、C的坐标.
(2)设CD交x轴于点E,根据△OCD的面积即可求出CD的长度从而求出点D的坐标.
(3)将点D的坐标代入反比例函数的解析式中即可求出k的值.
解答 解:(1)令x=0代入y=$\frac{1}{2}$x-2,
∴y=-2,
∴B(0,-2),
令y=0代入y=$\frac{1}{2}$x-2,
∴x=4,
∴A(4,0)
令y=-1代入y=$\frac{1}{2}$x-2,
∴x=2,
∴C(2,-1)
(2)设CD交x轴于点E,
∵CD∥y轴,
∴OE=2,
∵S△OCD=$\frac{5}{2}$,
∴$\frac{1}{2}$OE•CD=$\frac{5}{2}$,
∴CD=$\frac{5}{2}$,
∴D的纵坐标为:$\frac{5}{2}$-1=$\frac{3}{2}$,
∴D的坐标为:(2,$\frac{3}{2}$)
(3)将点D(2,$\frac{3}{2}$)代入y=$\frac{k}{x}$,
∴k=2×$\frac{3}{2}$=3,
点评 本题考查反比例函数的解析式,解题的关键是根据直线的解析式求出点A、B、C的坐标,本题属于基础题型.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
6.(1)图(1)是正方体木块,把它切去一块,可能得到形如图(2),(3),(4),(5)的木块.

我们知道,图(1)的正方体木块有8个顶点,12条棱,6个面,请你将图(2),(3),(4),(5)中木块的顶点数,棱数,面数填入表:
(2)观察表,请你归纳上述各种木块的顶点数,棱数,面数之间的数量关系,这种数量关系是:
顶点数+面数-2=棱数.
(3)图⑥是用虚线画出的正方体木块,请你想象一种与图②~⑤不同的切法,把切去一块后得到的那一块的每条棱都改画成实线,则该木块的顶点数为8,棱数为12,面数为6.这与你(2)题中所归纳的关系是否相符?


我们知道,图(1)的正方体木块有8个顶点,12条棱,6个面,请你将图(2),(3),(4),(5)中木块的顶点数,棱数,面数填入表:
| 图 | 顶点数 | 棱数 | 面数 |
| (1) | 8 | 12 | 6 |
| (2) | 6 | 9 | 5 |
| (3) | 8 | 12 | 6 |
| (4) | 8 | 13 | 7 |
| (5) | 10 | 15 | 7 |
顶点数+面数-2=棱数.
(3)图⑥是用虚线画出的正方体木块,请你想象一种与图②~⑤不同的切法,把切去一块后得到的那一块的每条棱都改画成实线,则该木块的顶点数为8,棱数为12,面数为6.这与你(2)题中所归纳的关系是否相符?

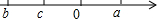 (1)实数a,b,c在数轴上的对应点如图所示,化简$\root{3}{{a}^{3}}$+|a+b|-$\sqrt{{c}^{2}}$-|b-c|.
(1)实数a,b,c在数轴上的对应点如图所示,化简$\root{3}{{a}^{3}}$+|a+b|-$\sqrt{{c}^{2}}$-|b-c|.